Trong quá trình ông An xây nhà thì phải đổ bê tông cho một

Câu hỏi số 782165:

Vận dụng

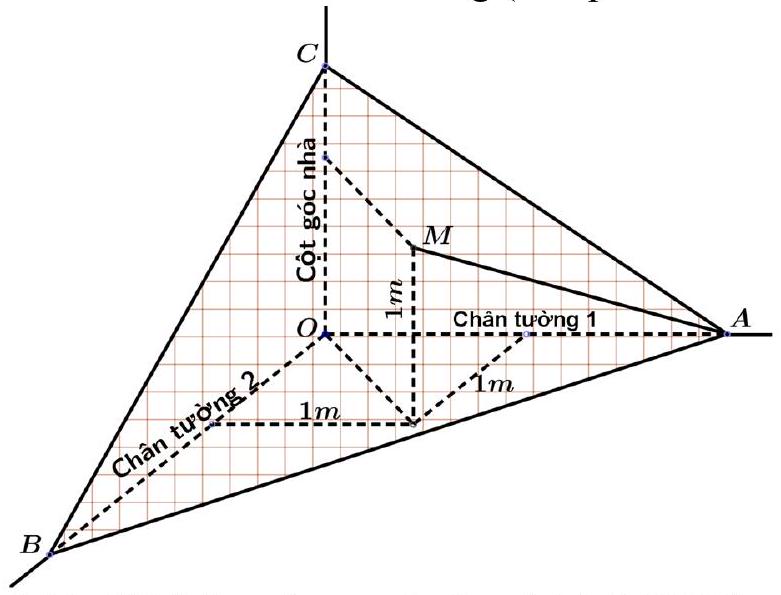
Trong quá trình ông An xây nhà thì phải đổ bê tông cho một mái vát để lợp ngói. Ông tính toán việc ghép cốt pha đi qua điểm $B$ trên một chân tường và điểm $C$ trên cột góc nhà và tận dụng một chiếc cột có sẵn cách đều hai bức tường $1m$ và chiều cao $1m$ (đỉnh cột là điểm $M$) để chống mặt ghép, đồng thời mặt ghép cốt pha phải đi qua điểm $A$ trên một chân tường còn lại cách điểm $O$ một khoảng $2m$ (tham khảo hình vẽ). Biết rằng hai bức tường được xây vuông góc với nhau, mỗi bức tường đều vuông góc với sàn mái nhà. Diện tích nhỏ nhất của khung ghép cốt pha $ABC$ là bao nhiêu mét vuông (kết quả làm tròn đến hàng phần mười) ?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:782165

Phương pháp giải

Giả sử $\left( {ABC} \right)$ đi qua $A\left( {2,0,0} \right),B\left( {0,b,0} \right),C\left( {0,0,c} \right)$

Từ điều kiện$\left( {ABC} \right)$ đi qua điểm $M\left( {1,1,1} \right)$ tìm liên hệ b, c và điều kiện của bc

Tính diện tích tam giác ABC bằng $S_{\Delta ABC} = \dfrac{1}{2}\left| \left\lbrack {\overset{\rightarrow}{AB},\overset{\rightarrow}{AC}} \right\rbrack \right|$ và tìm GTNN

Giải chi tiết

Giả sử $\left( {ABC} \right)$ đi qua $A\left( {2,0,0} \right),B\left( {0,b,0} \right),C\left( {0,0,c} \right)$

Khi đó $\left( {ABC} \right):\dfrac{x}{2} + \dfrac{y}{b} + \dfrac{z}{c} = 1$

Do $\left( {ABC} \right)$ đi qua điểm $M\left( {1,1,1} \right)$ nên $\left. \dfrac{1}{2} + \dfrac{1}{b} + \dfrac{1}{c} = 1\Leftrightarrow\dfrac{1}{b} + \dfrac{1}{c} = \dfrac{1}{2}\Leftrightarrow bc = 2\left( {b + c} \right) \right.$

$\begin{array}{l} \left. \Rightarrow b^{2}c^{2} = 4\left( {b^{2} + c^{2} + 2bc} \right) \geq 4\left( {2bc + 2bc} \right) \right. \\ \left. \Leftrightarrow b^{2}c^{2} \geq 16bc \right. \\ \left. \Leftrightarrow bc \geq 16 \right. \end{array}$

Ta có $\left. \overset{\rightarrow}{AB} = \left( {- 2,b,0} \right);\overset{\rightarrow}{AC}\left( {- 2,0,c} \right)\Rightarrow\left\lbrack {\overset{\rightarrow}{AB},\overset{\rightarrow}{AC}} \right\rbrack = \left( {bc,2c,2b} \right) \right.$

$\begin{array}{l} \left. \Rightarrow S_{\Delta ABC} = \dfrac{1}{2}\left| \left\lbrack {\overset{\rightarrow}{AB},\overset{\rightarrow}{AC}} \right\rbrack \right| = \dfrac{1}{2}\sqrt{b^{2}c^{2} + 4\left( {b^{2} + c^{2}} \right)} = \sqrt{b^{2} + c^{2} + \dfrac{b^{2}c^{2}}{4}} \right. \\ {= \sqrt{\left( {b + c} \right)^{2} - 2bc + \dfrac{b^{2}c^{2}}{4}} = \sqrt{\dfrac{b^{2}c^{2}}{4} - 2bc + \dfrac{b^{2}c^{2}}{4}} = \sqrt{\dfrac{b^{2}c^{2}}{2} - 2bc}} \end{array}$

Xét $f(x) = \dfrac{x^{2}}{2} - 2x$ với $\left. x \geq 16\Rightarrow f_{\min} = f(16) = 96 \right.$

$\left. \Rightarrow S_{\min} = \sqrt{96} \approx 9,8 \right.$

Đáp án cần điền là: 9,8

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.