Hai rô bốt giao hàng tự động giống nhau cùng xuất phát từ các vị

Câu hỏi số 782167:

Vận dụng cao

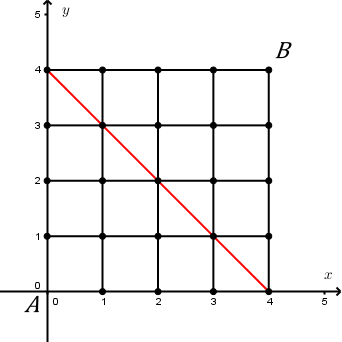
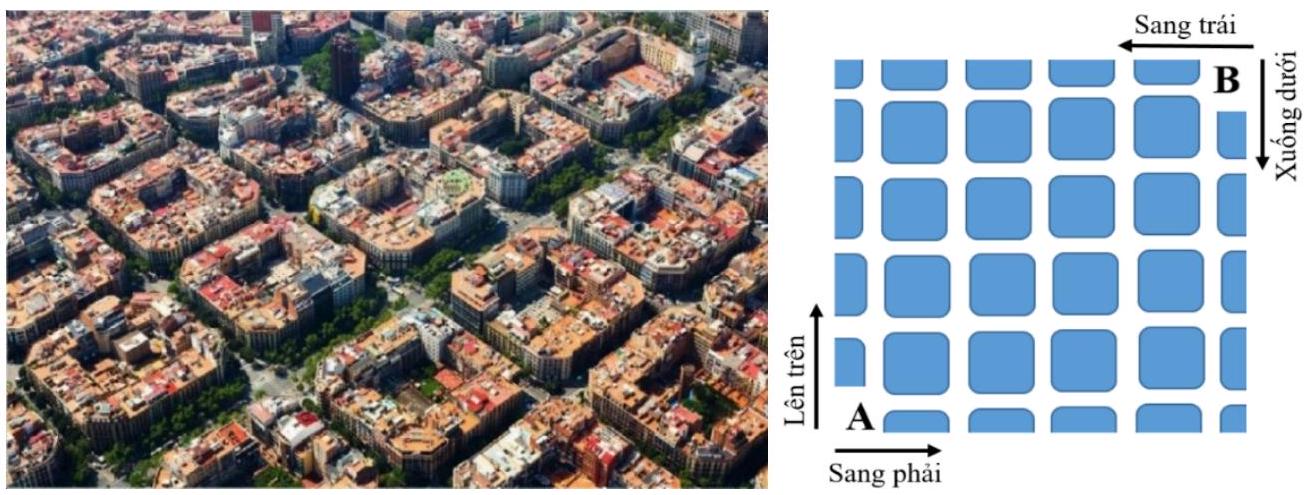
Hai rô bốt giao hàng tự động giống nhau cùng xuất phát từ các vị trí $A$ và $B$ của một khu đô thị được quy hoạch ô bàn cờ (tham khảo hình vẽ). Mỗi tuyến phố trong khu đô thị coi như một cạnh của một hình vuông. Rô bốt xuất phát từ vị trí $A$ chỉ có thể di chuyển sang phải hoặc lên trên, rô bốt xuất phát từ vị trí $B$ chỉ có thể di chuyển sang trái hoặc xuống dưới (với xác suất như nhau mỗi khi có sự lựa chọn). Hai rô bốt đều di chuyển đến điểm xuất phát của nhau. Biết rằng tốc độ di chuyển của hai rô bốt là như nhau, xác suất để hai rô bốt gặp nhau tại một điểm nào đó trong hành trình của mình bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:782167

Phương pháp giải

Gắn hệ trục toạ độ, xác định toạ độ các điểm mà robot gặp nhau từ đó tính các cách để robot đi

Giải chi tiết

Gắn hệ trục toạ độ như hình vẽ với robot A xuất phát từ $O\left( {0,0} \right)$ và $B\left( {4,4} \right)$

Khi A di chuyển sang phải hoặc lên trên nên số cách đi của A là $0 + x + 0 + y = x + y$

Khi B di chuyển sang trái hoặc xuống dưới nên số cách đi của B là $4 - x + 4 - y = 8 - x - y$

với $x,y \in Z,0 \le x,y \le 4$

Vì 2 robot gặp nhau nên $x + y = 8 - x - y \Leftrightarrow x + y = 4$

Khi đó các bộ $\left( {x,y} \right) \in \left\{ {\left( {0,4} \right),\left( {1,3} \right),\left( {2,2} \right),\left( {3,1} \right),\left( {4,0} \right)} \right\}$

TH1: Nếu 2 robot gặp nhau tại $\left( {0,4} \right)$ hoặc $\left( {4,0} \right)$ thì mỗi robot chỉ có 1 cách đi

TH2: Khi 2 robot gặp nhau tại $\left( {3,1} \right)$ hoặc $\left( {1,3} \right)$ thì mỗi robot có $C_4^1.C_3^3 = 4$ cách đi đến điểm gặp nhau và thêm 4 cách đi đến đích. Vậy 2 robot có $4.4.4.4 = 256$cách

TH3: Khi 2 robot gặp nhau tạ $\left( {2,2} \right)$ thì mỗi robot có $C_4^2.C_2^2 = 6$ cách đi đến điểm gặp nhau và thêm 6 cách đi đến đích. Vậy 2 robot có ${6^4} = 1296$cách

Tổng số cách đi của mỗi robot để gặp nhau trên đường đến đích là $1.2 + 2.256 + 1296 = 1810$

Không gian mẫu $\left| \Omega \right| = C_8^4.C_4^4.C_8^4.C_4^4 = 4900$

Vậy xác suất để 2 robot gặp nhau là $\dfrac{{1810}}{{4900}} \approx 0,37$

Đáp án cần điền là: 0,37

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.