Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Hai hồ bơi được nối với nhau bởi một con kênh dài 200 m, rộng 8 m (là khoảng cách giữa hai

Câu hỏi số 785812:
Vận dụng

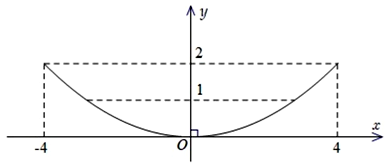
Hai hồ bơi được nối với nhau bởi một con kênh dài 200 m, rộng 8 m (là khoảng cách giữa hai mép bờ kênh), sâu 2 m (tính từ điểm thấp nhất của đáy kênh đến mặt đất chứa hai bờ kênh). Mặt cắt đứng của con kênh được mô hình hóa bởi một phần parabol có phương trình $y = f(x) = ax^{2} + bx + c$ (với $a > 0$ ); xét mặt phẳng chứa parabol đó với hệ trục tọa độ $Oxy$, đơn vị mỗi trục tọa độ là mét, trục $Ox$ tiếp xúc với parabol đó, trục $Oy$ vuông góc với mặt đất, chứa trục đối xứng của parabol đó và có chiều dương hướng lên trời (xem hình minh họa ở dưới).

Đúng Sai
a) Parabol đó đi qua điểm $\left( {4;2} \right)$ và có đỉnh $O\left( {0;0} \right)$.
b) Parabol đó có phương trình $y = f(x) = \dfrac{x^{2}}{8}$.
c) Diện tích mặt cắt của con kênh bằng $\dfrac{16}{3}$ m2.
d) Vào mùa hè, mực nước trong kênh cao 1 m (tính từ điểm thấp nhất của đáy kênh đến mặt nước). Lượng nước trong kênh vào mùa hè bằng 754 m3 (kết quả làm tròn đến hàng đơn vị).

Đáp án đúng là: Đ; Đ; S; Đ

Quảng cáo

Xem lời giải
Câu hỏi:785812
Phương pháp giải

Parabol đó có phương trình $y = f(x) = ax^{2} + bx + c$ . Từ các điểm mà parabol đi qua xác định các hệ số

Tính diện tích, thể tích bằng tích phân

Giải chi tiết

a) Đúng. Từ hình vẽ thì parabol đó đi qua điểm $\left( {4;2} \right)$ và có đỉnh $O\left( {0;0} \right)$.

b) Đúng. Parabol đó có phương trình $y = f(x) = ax^{2} + bx + c$ đi qua điểm $\left( {4;2} \right)$ và có đỉnh $O\left( {0;0} \right)$ nên $\left. \left\{ \begin{array}{l} {2 = a \cdot 4^{2} + b \cdot 4 + c} \\ {0 = a \cdot 0^{2} + b \cdot 0 + c} \\ {\dfrac{- b}{2a} = 0} \end{array} \right.\Rightarrow b = c = 0,a = \dfrac{1}{8} \right.$.

c) Sai. Mặt cắt của con kênh là hình phẳng giới hạn bởi hai đồ thị hàm số $y = \dfrac{x^{2}}{8},y = 2$ và hai đường thẳng $x = - 4,x = 4$ nên diện tích bằng ${\int\limits_{- 4}^{4}\left| {\dfrac{x^{2}}{8} - 2} \right|}dx = {\int\limits_{- 4}^{4}\left( {2 - \dfrac{x^{2}}{8}} \right)}dx = \left. \left( {2x - \dfrac{x^{3}}{24}} \right) \right|_{- 4}^{4} = \dfrac{32}{3}$m2.

d) Đúng. $\left. \dfrac{x^{2}}{8} = 1\Leftrightarrow x^{2} = 8\Leftrightarrow x = \pm 2\sqrt{2} \right.$. Lượng nước trong kênh vào mùa hè bằng $200{\int\limits_{- 2\sqrt{2}}^{2\sqrt{2}}\left| {\dfrac{x^{2}}{8} - 1} \right|}dx = 200{\int\limits_{- 2\sqrt{2}}^{2\sqrt{2}}\left( {1 - \dfrac{x^{2}}{8}} \right)} = \left. {200\left( {x - \dfrac{x^{3}}{24}} \right)} \right|_{- 2\sqrt{2}}^{2\sqrt{2}} = \dfrac{1600\sqrt{2}}{3} \approx 754$ m3

Đáp án cần chọn là: Đ; Đ; S; Đ

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn