Trên công trường xây dựng, một công nhân muốn tạo ra một dụng cụ để

Câu hỏi số 787192:

Vận dụng

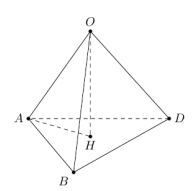
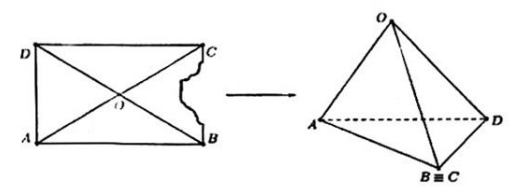
Trên công trường xây dựng, một công nhân muốn tạo ra một dụng cụ để đựng vật liệu lỏng từ một tấm thép hình chữ nhật $ABCD$ tâm $O$ có $AB = 3,2m,\,\, AD = 2,4m$. Do tấm thép bị hỏng một phần (tham khảo hình vẽ) nên người đó cắt bỏ tam giác $OBC$ và hàn hai mép $OB,\,\, OC$ với nhau để thu được một hình tứ diện $OABD$ (không có mặt $ABD$). Dụng cụ này sẽ được vùi đất xung quanh sao cho đỉnh $O$ quay xuống và mặt $ABD$ hướng lên trên, khi đựng đầy vật liệu lỏng thì phần không gian trong lòng của dụng cụ hoàn toàn bị lấp đầy. Tính thể tích của vật liệu lỏng được đựng đầy trong dụng cụ. (Kết quả làm tròn đến hàng phần chục của đơn vị $m^{3}$ và xem độ dày của tấm thép không đáng kể).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:787192

Phương pháp giải

Sử dụng công thức Herone tính diện tích tam giác đáy $ABD$

Gọi $H$ là hình chiếu vuông góc của $O$ lên mặt phẳng $ABD$

Tính $HA = \dfrac{AB.BD.DA}{4S_{ABD}}$, sau đó tính $OH$

Giải chi tiết

Xét tam giác $ABD$ có $AB = BD = 3,2(m),\,\, AD = 2,4(m)$ nên

$S_{ABD} = \sqrt{p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{12\sqrt{55}}{25}$

Gọi $H$ là hình chiếu vuông góc của $O$ lên $\left( {ABD} \right)$

Vì $OA = OB = OD$ nên $H$ là tâm đường tròn ngoại tiếp tam giác $ABD$

Khi đó $HA = \dfrac{AB.BD.DA}{4S_{ABD}} = \dfrac{3,2.3,2.2,4}{4.\dfrac{12\sqrt{55}}{25}} = \dfrac{64\sqrt{55}}{275}$

Hơn nữa $OA = \dfrac{1}{2}\sqrt{AB^{2} + AD^{2}} = \dfrac{1}{2}\sqrt{3,2^{2} + 2,4^{2}} = 2$

Do đó $OH = \sqrt{OA^{2} - HA^{2}} = \sqrt{\dfrac{1404}{1375}}$

Thể tích của vật liệu lỏng được đựng đầy trong dụng cụ là $V = \dfrac{1}{3}S_{ABD}.OH = \dfrac{1}{3}.\dfrac{12\sqrt{55}}{275}.\sqrt{\dfrac{1404}{1375}} \approx 1,2$

Đáp án cần điền là: 1,2

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.