Trong một trung tâm logistics, người ta cần thiết kế một thùng hàng hình hộp

Câu hỏi số 789559:

Vận dụng

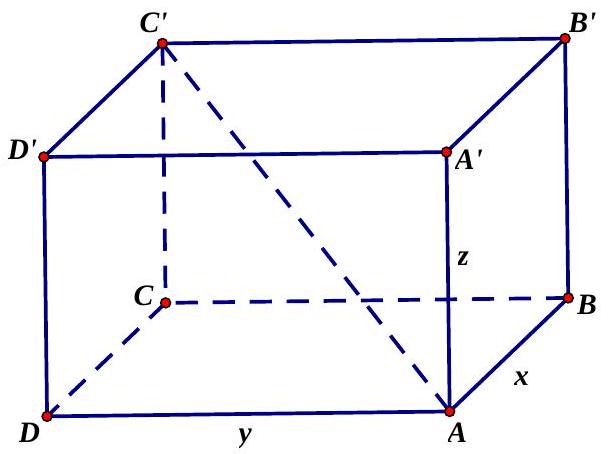
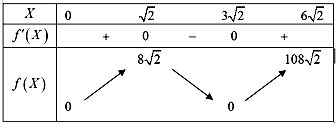
Trong một trung tâm logistics, người ta cần thiết kế một thùng hàng hình hộp chữ nhật để đóng gói và vận chuyển thiết bị điện tử. Tổng diện tích các mặt ngoài của thùng bằng $36\text{m}^{2}$ (bao gồm cả mặt đáy, mặt nắp và 4 mặt bên). Để đảm bảo khả năng đóng gói vừa vặn thiết bị, đường chéo không gian của thùng phải dài 6 mét. Thể tích lớn nhất có thể của thùng hàng này là bao nhiêu (tính theo đơn vị mét khối, làm tròn đến hàng phần chục)?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:789559

Phương pháp giải

Định lý Vi-ét cho phương trình bậc 3

Nếu $x_{1},x_{2},x_{3}$ là ba nghiệm của phương trình bậc ba $ax^{3} + bx^{2} + cx + d = 0(a \neq 0)$, thì $\begin{cases} {x_{1} + x_{2} + x_{3}} & {= - \dfrac{b}{a}} \\ {x_{1}x_{2} + x_{2}x_{3} + x_{3}x_{1}} & {= \dfrac{c}{a}} \\ {x_{1} \cdot x_{2} \cdot x_{3}} & {= - \dfrac{d}{a}} \end{cases}$

Giải chi tiết

Gọi $x,y,z$ lần lượt là độ dài của các cạnh $AB,AD,AA'$.

Diện tích tất cả các mặt là $\left. \text{S}_{\text{tp}} = 2\left( {xy + yz + zx} \right) = 36\Leftrightarrow xy + yz + zx = 18 \right.$ (1).

Độ dài đường chéo $\left. AC' = \sqrt{x^{2} + y^{2} + z^{2}} = 6\Leftrightarrow x^{2} + y^{2} + z^{2} = 36 \right.$.

Suy ra $\left. {(x + y + z)}^{2} = x^{2} + y^{2} + z^{2} + 2\left( {xy + yz + zx} \right) = 72\Leftrightarrow x + y + z = 6\sqrt{2} \right.$ (2).

Thể tích của khối hộp chữ nhật là $V = xyz$ (3).

Từ (1), (2) và (3) suy ra $x,y,z$ là 3 nghiệm của phương trình

$\begin{matrix} \left. X^{3} - 6\sqrt{2}X^{2} + 18X - V = 0\Leftrightarrow V = X^{3} - 6\sqrt{2}X^{2} + 18X \right. \end{matrix}$ $(4)$

Bảng biến thiên của hàm số $f(X) = X^{3} - 6\sqrt{2}X^{2} + 18X$ trên $\left( {0;6\sqrt{2}} \right)$ như sau

Dựa vào bảng biến thiên, giá trị lớn nhất của $V$ để phương trình (4) có 3 nghiệm (không cần phân biệt) trên khoảng $\left( {0;6\sqrt{2}} \right)$ là $8\sqrt{2}$.

Vậy thể tích của khối hộp chữ nhật lớn nhất là $8\sqrt{2} \approx 11,3m^{3}$ khi $\left( {x;y;z} \right) = \left( {\sqrt{2};4\sqrt{2};\sqrt{2}} \right)$ và các hoán vị của nó.

Đáp án cần điền là: 11,3

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.