Trong một cuộc diễn tập phòng không, một bệ phóng tên lửa phòng

Câu hỏi số 790448:

Thông hiểu

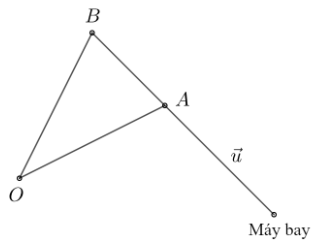
Trong một cuộc diễn tập phòng không, một bệ phóng tên lửa phòng không được đặt tại vị trí $O\left( {0;0;0} \right)$ (trong không gian $Oxyz$ với đơn vị trên các hệ trục tính theo ki – lô – mét) có tầm bắn tối đa là 30km và tên lửa được phóng ra với vận tốc không đổi là 500m/s. Một máy bay không người lái bay theo một đường thẳng có vec tơ chỉ phương $\overset{\rightarrow}{u} = \left( {3; - 4;0} \right)$ với vận tốc không đổi là 900km/h. Khi phát hiện máy bay không người lái tại vị trí $A\left( {6; - 20;16} \right)$ thì tên lửa rời bệ phóng, khai hỏa và đã bắn hạ được mục tiêu. Hỏi khoảng cách từ bệ phóng tên lửa đến vị trí máy bay không người lái bị bắn hạ bằng bao nhiêu ki – lô – mét (giả sử cả máy bay không người lái và tên lửa đều bay theo đường thẳng và không chịu tác động của trọng lực hay lực cả không khí)

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:790448

Phương pháp giải

Gọi B là vị trí máy bay rơi. Từ vận tốc máy bay và tên lửa suy ra $OB = 2AB$

Gọi $\alpha = \left( {\overset{\rightarrow}{OA},\overset{\rightarrow}{u}} \right)$. Xét 2 trường hợp góc $\alpha = \left( {\overset{\rightarrow}{OA},\overset{\rightarrow}{u}} \right)$ nhọn, tù để tính OB

Giải chi tiết

Gọi $B$ là vị trí mà tên máy bay rơi

Đổi $500m/s = 1800km/h$

Gọi $v_{1},\,\, v_{2}$ lần lượt là vận tốc của tên lửa và máy bay không người lái

Khi đó $v_{1} = 2v_{2}$

Ta có: $\left. OB = v_{1}t,\,\, AB = v_{2}t\Rightarrow OB = 2AB \right.$

Đặt $\left. AB = x\Rightarrow OB = 2x \right.$

Ta có: $OA = \sqrt{6^{2} + 20^{2} + 16^{2}} = 2\sqrt{173}$

Gọi $\alpha = \left( {\overset{\rightarrow}{OA},\overset{\rightarrow}{u}} \right)$

Trường hợp 1: $\alpha$ nhọn

Ta có: $\overset{\rightarrow}{OA} = \left( {6; - 20;16} \right),\,\,\overset{\rightarrow}{u} = \left( {3; - 4;0} \right)$

Suy ra $\cos\left( {\overset{\rightarrow}{OA},\overset{\rightarrow}{u}} \right) = \dfrac{98}{2\sqrt{173}.5}$

Áp dụng định lý cosin vào tam giác $OAB$ ta được $\cos\alpha = \dfrac{AB^{2} + OA^{2} - OB^{2}}{2AB.AO} = \dfrac{x^{2} + 692 - 4x^{2}}{2\sqrt{173}.2x}$

Như vậy

$\begin{array}{l} {\dfrac{692 - 3x^{2}}{2\sqrt{173}.2x} = \dfrac{98}{2\sqrt{173}.5}} \\ \left. \Leftrightarrow - 196x = - 15x^{2} + 3460 \right. \\ \left. \Leftrightarrow 15x^{2} - 196x - 3460 = 0 \right. \\ \left. \Leftrightarrow\left\lbrack \begin{array}{l} {x = \dfrac{346}{15}} \\ {x = - 10} \end{array} \right. \right. \end{array}$

Trường hợp 2: $\alpha$ tù

Tương tự như trên ta tìm được $\left\lbrack \begin{array}{l} {x = 10} \\ {x = - \dfrac{346}{15}} \end{array} \right.$

Vậy $\left. x = 10\Rightarrow OB = 20\left( {tm} \right) \right.$

Đáp án cần điền là: 20

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.