Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Một tia sáng truyền từ không khí vào một vật liệu chế tạo thành

Câu hỏi số 798784:
Vận dụng

Một tia sáng truyền từ không khí vào một vật liệu chế tạo thành khối lăng kính hình hộp chữ nhật. Tia sáng được phát theo hướng $\vec{v}=\langle -2 ;-3 ;-6\rangle$ từ nguồn sáng tại điểm $P(2,2,4)$. Khối lăng kính được đặt sao cho tia sáng đi qua lăng kính, nhận tại điểm $Q$ và rời ra tại điểm $R$, rồi được bẻ khỏi một cạnh bên tại điểm $S(-5,-6,-7)$. Góc nhọn giữa $P Q$ và pháp tuyến của mặt trên lăng kính tại $Q$ là $\theta$, và góc nhọn giữa $Q R$ và cùng một pháp tuyến đó là $\beta$ (xem hình bên). Cho biết mặt trên của lăng kính là một phần của mặt phẳng $x+y+z=1$ và đáy của lăng kính là một phần của mặt phẳng $x+$ $y+z=-9$. Ngoài ra, tia sáng trên đoạn $P Q$ song song với tia sáng trên đoạn $R S$, và bốn điểm $P, Q, R, S$ nằm trong cùng một mặt phẳng. (tham khảo hình vẽ dưới đây)

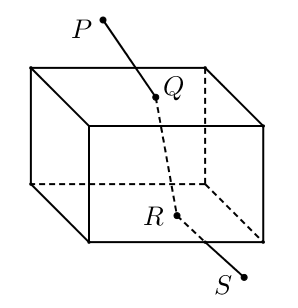
Đúng Sai
a) Độ dày của lăng kính đo theo phương pháp tuyến tại $Q$ bằng $\dfrac{10 \sqrt{3}}{3}$
b) $\cos \theta<\cos \beta$.
c) $Q R=\dfrac{5 \sqrt{170}}{17}$
d) Định luật khúc xạ (Snell) cho biết $\sin \theta=k \sin \beta$ trong đó $k$ là hằng số khúc xạ của vật liệu. Từ đó suy ra hằng số khúc xạ của vật liệu làm lăng kính này là $\dfrac{\sqrt{170}}{7}$.

Đáp án đúng là: Đ; S; Đ; S

Quảng cáo

Xem lời giải
Câu hỏi:798784
Phương pháp giải

a) Độ dày của lăng kính bằng khoảng cách giữa hai mặt phẳng

b) Tìm toạ độ Q là giao điểm của PQ với mặt phẳng \(x + y + z = 1\) và toạ độ R là giao điểm của RS với \(x + y + z =  - 9\). Từ đó tính QR

c) Tính \(\sin \left( \theta  \right) = \sin \left( {\vec u,\vec n} \right)\) và \(\sin \left( \beta  \right) = \sin \left( {\overrightarrow {QR} ,\vec n} \right)\) sau đó so sánh.

d) Từ \(\sin \left( \theta  \right) = k.\sin \beta \) tìm k

Giải chi tiết

a) Đúng. Độ dày của lăng kính bằng khoảng cách giữa hai mặt phẳng và bằng \(\dfrac{{\left| {1 + 9} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \dfrac{{10\sqrt 3 }}{3}\)

b) Sai. VTPT của hai mặt phẳng là \(\overrightarrow n = \left( {1,1,1} \right)\)

Gọi \(Q\left( {2 - 2t,2 - 3t,4 - 6t} \right) \in x + y + z = 1 \Rightarrow t = \dfrac{7}{{11}} \Rightarrow Q\left( {\dfrac{8}{{11}},\dfrac{1}{{11}},\dfrac{2}{{11}}} \right)\)

Do \(RS\parallel PQ\) nên \(\overrightarrow {RS} \) cùng hướng với \(\overrightarrow v \left( { - 2, - 3, - 6} \right)\)

Phương trình đường thẳng RS qua \(S\left( { - 5, - 6, - 7} \right)\) và có VTCP \(\overrightarrow v \left( { - 2, - 3, - 6} \right)\) là \(\left\{ \begin{array}{l}x =  - 5 - 2t\\y =  - 6 - 3t\\z =  - 7 - 6t\end{array} \right.\)

Gọi \(R\left( { - 5 - 2t; - 6 - 3t; - 7 - 6t} \right)\)

Do \(R \in x + y + z =  - 9 \Rightarrow t = \dfrac{{ - 9}}{{11}} \Rightarrow R\left( {\dfrac{{ - 37}}{{11}};\dfrac{{ - 39}}{{11}};\dfrac{{ - 23}}{{11}}} \right)\)

\( \Rightarrow \overrightarrow {QR} = \left( { - \dfrac{{45}}{{11}};\dfrac{{ - 40}}{{11}};\dfrac{{ - 25}}{{11}}} \right) = - \dfrac{5}{{11}}\left( {9,8,5} \right)\)

\( \Rightarrow \sin \left( \theta \right) = \sin \left( {\overrightarrow u ,\overrightarrow n } \right) = \dfrac{{\left| { - 2 - 3 - 6} \right|}}{{\sqrt {49} .\sqrt 3 }} = \dfrac{{11\sqrt 3 }}{{21}} \Rightarrow \cos \left( \theta \right) = 0,42\)

\( \Rightarrow \sin \left( \beta \right) = \sin \left( {\overrightarrow {QR} ,\overrightarrow n } \right) = \dfrac{{9 + 8 + 5}}{{\sqrt {{9^2} + {8^2} + {5^2}} .\sqrt 3 }} = 0,97 \Rightarrow \cos \left( \beta \right) = 0,225\)

\( \Rightarrow \cos \theta > \cos \beta \)

c) Đúng. \(\overrightarrow {QR} = \left( { - \dfrac{{45}}{{11}};\dfrac{{ - 40}}{{11}};\dfrac{{ - 25}}{{11}}} \right) = - \dfrac{5}{{11}}\left( {9,8,5} \right) \Rightarrow QR = \dfrac{{5\sqrt {170} }}{{11}}\)

d) Sai. Do \(\sin \left( \theta \right) = k.\sin \beta \Leftrightarrow \dfrac{{11\sqrt 3 }}{{21}} = k.\dfrac{{22}}{{\sqrt {170} .\sqrt 3 }} \Rightarrow k = \dfrac{{\sqrt {170} }}{{14}}\)

Đáp án cần chọn là: Đ; S; Đ; S

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn