Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

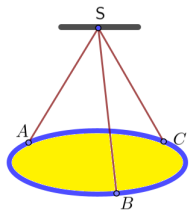
Một chiếc đĩa kim loại khối lượng 4,5 kg được treo bởi ba sợi dây không dãn SA, SB, SC sao cho

Câu hỏi số 825174:
Thông hiểu

Một chiếc đĩa kim loại khối lượng 4,5 kg được treo bởi ba sợi dây không dãn SA, SB, SC sao cho SABC là hình chóp đều có $\widehat{ASB} = 60^{{^\circ}}$ (hình vẽ). Khối lượng dây không đáng kể; lực căng của mỗi sợi dây SA, SB, SC đặt tại điểm S tương ứng là ${\overset{\rightarrow}{F}}_{1},{\overset{\rightarrow}{F}}_{2},{\overset{\rightarrow}{F}}_{3}$ có độ lớn bằng nhau. Lấy độ lớn của gia tốc trọng trường $\left| \overset{\rightarrow}{g} \middle| = 9,8\left( {~\text{m}/\text{s}^{2}} \right) \right.$. Xét đúng sai của các khẳng định sau

Đúng Sai
a) Trọng lực $\overset{\rightarrow}{P}$ của hệ vật có độ lớn bằng $34,3(\text{N})$.
b) ${\overset{\rightarrow}{F}}_{1}.{\overset{\rightarrow}{F}}_{2} \neq \overset{\rightarrow}{F_{1}}.{\overset{\rightarrow}{F}}_{3}$.
c) Độ lớn của các lực $\overset{\rightarrow}{F_{1}},\overset{\rightarrow}{F_{2}},\overset{\rightarrow}{F_{3}}$ bằng $14,7(\text{N})$.

Đáp án đúng là: S; S; S

Quảng cáo

Xem lời giải
Câu hỏi:825174
Phương pháp giải

Áp dụng công thức $\overset{\rightarrow}{a}.\overset{\rightarrow}{b} = \left| \overset{\rightarrow}{a} \right|.\left| \overset{\rightarrow}{b} \right|.\cos\left( {\overset{\rightarrow}{a},\overset{\rightarrow}{b}} \right)$

$F = \sqrt{F_{1}^{2} + F_{2}^{2} + F_{3}^{2} + 2F_{1}F_{2}\cos\left( {F_{1},F_{2}} \right) + 2F_{1}F_{3}\cos\left( {F_{1},F_{3}} \right) + 2F_{2}F_{3}\cos\left( {F_{2},F_{3}} \right)}$

Giải chi tiết

a) Sai. Ta có $P = mg = 9,8.4,5 = 44,1$N

b) Sai. Vì ${\overset{\rightarrow}{F}}_{1},{\overset{\rightarrow}{F}}_{2},{\overset{\rightarrow}{F}}_{3}$ có độ lớn bằng nhau và các góc $\angle ASB = \angle BSC = \angle CSA = 60^{0}$

Khi đó ${\overset{\rightarrow}{F}}_{1}.{\overset{\rightarrow}{F}}_{2} = \overset{\rightarrow}{F_{1}}.{\overset{\rightarrow}{F}}_{3}$

c) $F = \sqrt{F_{1}^{2} + F_{2}^{2} + F_{3}^{2} + 2F_{1}F_{2}\cos\left( {F_{1},F_{2}} \right) + 2F_{1}F_{3}\cos\left( {F_{1},F_{3}} \right) + 2F_{2}F_{3}\cos\left( {F_{2},F_{3}} \right)}$

$= \sqrt{3F_{1}^{2} + 3.2F_{1}^{2}.\cos 60^{0}} = F_{1}.\sqrt{6}$

Vì vật cân bằng nên $\overset{\rightarrow}{P} + {\overset{\rightarrow}{F}}_{1} + \overset{\rightarrow}{F_{2}} + \overset{\rightarrow}{F_{3}} = \overset{\rightarrow}{0}$

$\begin{array}{l} \left. \Rightarrow - \overset{\rightarrow}{P} = {\overset{\rightarrow}{F}}_{1} + \overset{\rightarrow}{F_{2}} + \overset{\rightarrow}{F_{3}} \right. \\ \left. \Leftrightarrow\left| \overset{\rightarrow}{P} \right| = \left| {{\overset{\rightarrow}{F}}_{1} + \overset{\rightarrow}{F_{2}} + \overset{\rightarrow}{F_{3}}} \right| \right. \\ \left. \Leftrightarrow 44,1 = F_{1}.\sqrt{6}\Rightarrow F_{1} = 18N \right. \end{array}$

Đáp án cần chọn là: S; S; S

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn