Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được

Câu hỏi số 828002:

Vận dụng

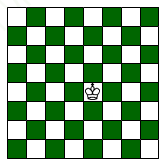
Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng (xem hình minh họa). Bạn An di chuyển quân vua ngẫu nhiên $3$ bước. Tính xác suất sau $3$ bước quân vua trở về ô xuất phát (Làm tròn đến hàng phần trăm)?

A green and white checkerboard with a crown

Description automatically generated

Quảng cáo

Xem lời giải

Câu hỏi:828002

Phương pháp giải

Chia hai trường hợp:

+ Từ ô ban đầu đi đến ô đen, đến đây có $4$ cách để đi bước hai rồi về lại vị trí ban đầu.

+ Từ ô ban đầu đi đến ô trắng, đến đây có $2$ cách để đi bước hai rồi về lại vị trí ban đầu.

Giải chi tiết

Tại mọi ô đang đứng, ông vua có $8$ khả năng lựa chọn để bước sang ô bên cạnh.

Do đó không gian mẫu $n(\Omega) = 8^{3}$.

Gọi $A$ là biến cố “sau 3 bước quân vua trở về ô xuất phát”.

Sau ba bước quân vua muốn quay lại ô ban đầu khi ông vua đi theo đường khép kín tam giác.

Chia hai trường hợp:

+ Từ ô ban đầu đi đến ô đen, đến đây có $4$ cách để đi bước hai rồi về lại vị trí ban đầu.

+ Từ ô ban đầu đi đến ô trắng, đến đây có $2$ cách để đi bước hai rồi về lại vị trí ban đầu.

Do số phần tử của biến cố A là $n(A) = 4.4 + 2.4 = 24$.

Vậy xác suất $P(A) = \dfrac{24}{8^{3}}$ $= \dfrac{3}{64}$.

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.