Dựa vào dữ liệu dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu của câu 26
Dựa vào dữ liệu dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu của câu 26 và câu 28.
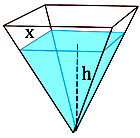
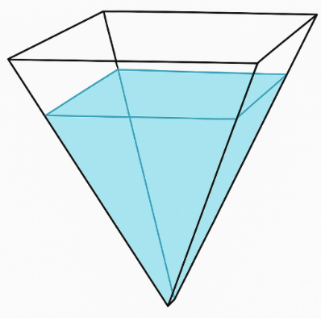
Một cái bể nước có dạng khối chóp tứ giác đều ngược với cạnh đáy bằng $3\sqrt{2}\,\, dm$ và chiều cao bằng $6\,\, dm$ (tham khảo hình vẽ bên). Nước được bơm vào bể với tốc độ không đổi là 2 lít/phút và ban đầu bể không chứa nước (các kết quả bên dưới được làm tròn đến hai chữ số thập phân sau dấu phẩy).
Trả lời cho các câu 1, 2, 3 dưới đây:
Thời gian để bể nước được bơm đầy là
Đáp án đúng là: A
Tính thể tích bể nước $V = \dfrac{1}{3}h.S$ từ đó tính thời gian đầy bể
Đáp án cần chọn là: A
Khi thể tích nước trong bể bằng $\dfrac{1}{3}$ thể tích của bể, tốc độ dâng lên của nước là
Đáp án đúng là: C
Tính thể tích bể nước theo chiều cao h ở thời điểm bất kì.
Lấy đạo hàm 2 vế từ đó tìm tốc độ dâng của nước.
Ta có $\left. \dfrac{h}{6} = \dfrac{x}{3\sqrt{2}}\Rightarrow x = \dfrac{\sqrt{2}h}{2} \right.$
$\left. \Rightarrow V = \dfrac{1}{3}\left( \dfrac{\sqrt{2}h}{2} \right)^{2}h = \dfrac{h^{3}}{6} \right.$
Tại thời điểm mà thể tích nước bằng $\dfrac{1}{3}$ thể tích bể thì $\left. \dfrac{1}{6}h^{3} = \dfrac{1}{3}.36 = 12\Rightarrow h = \sqrt[3]{72} \right.$dm
Lấy đạo hàm 2 vế của $V = \dfrac{h^{3}}{6}$ ta có
$\left. V'(t) = \dfrac{3h^{2}.h'(t)}{6}\Rightarrow h'(t) = \dfrac{6V'(t)}{3h^{2}} = \dfrac{6.2}{3.\left( \sqrt[3]{72} \right)^{2}} = 0,23 \right.$ dm/phút
Đáp án cần chọn là: C
Khi mực nước cách miệng bể 0,5 dm, người ta ngừng bơm và bắt đầu xả nước ra với ước lượng tốc độ giảm chiều cao của mực nước trong bể theo thời gian $t$ (phút) được mô hình hóa bởi hàm số $h'(t) = \dfrac{1}{350}t - \dfrac{193}{700}$ (dm/phút). Lượng nước xả ra sau 5 phút là
Đáp án đúng là: C
Tính chiều cao của mực nước khi lượng nước xả sau 5 phút
Lượng nước xả sau 5 phút là hiệu thể tích thời điểm chiều cao 5,5 và thời điểm mà nước xả 5 phút.
Đáp án cần chọn là: C
Quảng cáo
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
