Cho hình vuông \({C_1}\) có độ dài cạnh bằng 4. Người ta chia mỗi cạnh của

Câu hỏi số 847973:

Vận dụng

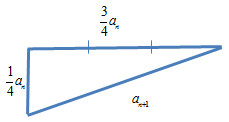
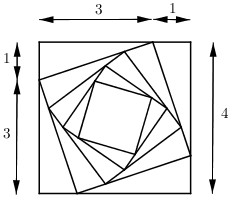
Cho hình vuông \({C_1}\) có độ dài cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để được hình vuông \({C_2}\)( tham khảo hình vẽ). Từ hình vuông \({C_2}\) tiếp tục làm như vậy để được hình vuông \({C_3}\),... . Tiếp tục quá trình trên ta được dãy các hình vuông \({C_1},{C_2},{C_3},...,{C_n}...\). Gọi \({S_1},{S_2},{S_3},...,{S_n}...\)tương ứng là diện tích các hình vuông \({C_1},{C_2},{C_3},...,{C_n}...\). Tính tổng \({S_1} + {S_2} + {S_3} + ... + {S_n} + ...\) (nhập kết quả dưới dạng phân số a/b)

Đáp án:

Đáp án đúng là: 128/3

Quảng cáo

Xem lời giải

Câu hỏi:847973

Phương pháp giải

Sử dụng công thức tính tổng của cấp số nhân lùi vô hạn \({S_n} = \dfrac{{{u_1}}}{{1 - q}}\) với \({u_1}\) là số hạng đầu tiên, \(q\) là công bội của cấp số nhân.

Giải chi tiết

Xét dãy \(\left( {{a_n}} \right)\) là độ dài cạnh của của dãy hình vuông \({C_1},{C_2},{C_3},...,{C_n}...\) với \({a_1} = 4\)

Ta có \({a_2} = \sqrt {{{\left( {\dfrac{1}{4}{a_1}} \right)}^2} + {{\left( {\dfrac{3}{4}{a_1}} \right)}^2}} {\rm{\;}} = \dfrac{{\sqrt {10} }}{4}{a_1}\)

…

\({a_{n + 1}} = \sqrt {{{\left( {\dfrac{1}{4}{a_n}} \right)}^2} + {{\left( {\dfrac{3}{4}{a_n}} \right)}^2}} {\rm{\;}} = \dfrac{{\sqrt {10} }}{4}{a_n}\)

Vậy dãy \(\left( {{a_n}} \right)\) lập thành cấp số nhân lùi vô hạn với công bội \(\dfrac{{\sqrt {10} }}{4}\)

Ta có \({S_{n + 1}} = {\left( {{a_{n + 1}}} \right)^2} = {\left( {{a_n}.\dfrac{{\sqrt {10} }}{4}} \right)^2} = {\left( {{a_n}} \right)^2}.\dfrac{5}{8} = {S_n}.\dfrac{5}{8}\)

Suy ra dãy \(\left( {{S_n}} \right)\) lập thành cấp số nhân lùi vô hạn với công bội \(q = \dfrac{5}{8}\) và \({S_1} = 16\)

Vậy \({S_1} + {S_2} + {S_3} + ... + {S_n} + ... = \dfrac{{{S_1}}}{{1 - q}} = \dfrac{{16}}{{1 - \dfrac{5}{8}}} = \dfrac{{128}}{3}\).

Đáp án cần điền là: 128/3

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.