Toán11
-
7 Chuyên đề
Cơ bản và nâng cao
-
8,260 bài tập
Hay và mới nhất theo chuyên đề
-
2,622,160 Lượt luyện
Luyện bài tập Môn Toán lớp 11
| Tên chuyên đề | Số bài tập | Dạng bài tập |
Đạo hàm |
0 bài tập | 0 dạng bài |
Vec tơ và quan hệ vuông góc |
17 bài tập | 0 dạng bài |
Quan hệ song song |
60 bài tập | 0 dạng bài |
Giới hạn |
0 bài tập | 0 dạng bài |
Dãy số - cấp số |
30 bài tập | 0 dạng bài |
Tổ hợp xác suất |
44 bài tập | 0 dạng bài |
Phương trình lượng giác |
32 bài tập | 0 dạng bài |
Câu 1
Cho tứ diện ABCD . Chứng minh rằng điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là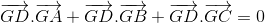 
Vec tơ và quan hệ vuông góc - Câu hỏi : 106832
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
Hoạt động mới nhất
-
phạm đình việt vừa hoàn thành câu hỏi “Mô đun của số phức \(z = 4 + i\) bằng”
-
Nguyễn Ngọc Phương Uyên vừa hoàn thành đề thi “Công thức tổng quát của alcohol no, đa ...”
-
Nep Te vừa gia nhập thành viên Tuyensinh247.com
-
Duy-hoang LE vừa hoàn thành đề thi “Gọi \(S\) là tập hợp tất cả các giá ...”
-
Đặng Tiến Minh vừa hoàn thành đề thi “Polime của este nào sau đây được dùng ...”
-
nguyenhiepductri vừa hoàn thành đề thi “Tính số gia của hàm số \(y = {x^2} + 2\) ...”
-
Trần Thu Uyên vừa hoàn thành đề thi “Hòa tan 6,3 gam hỗn hợp X gồm kim loại ...”
-
Lê Nguyễn Huyền Trân vừa gia nhập thành viên Tuyensinh247.com
-
Vũ Nguyễn Bảo Châu vừa hoàn thành đề thi “Khi một điện tích chuyển động vào ...”
-
MTP... vừa hoàn thành đề thi “Một hỗn hợp gồm 2 este đều đơn ...”
