Hai người tham gia một trò chơi di chuyển theo cạnh của các ô hình chữ nhật

Câu hỏi số 745275:

Vận dụng cao

Hai người tham gia một trò chơi di chuyển theo cạnh của các ô hình chữ nhật như trong hình (hình có \(15 \times 8\) ô hình chữ nhật nhỏ)

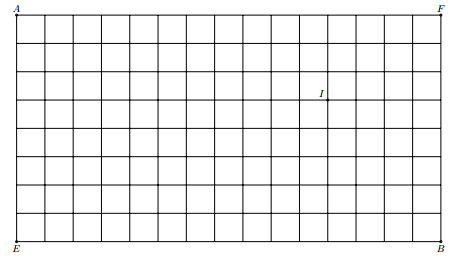
Người thứ nhất đi từ điểm \(A\) đến điểm \(B\), người thứ hai đi từ điểm \(E\) đến điểm \(F\). Biết rằng cả hai người cùng đi ngẫu nhiên và theo con đường ngắn nhất. Tính xác suất để cả hai người cùng đi qua điểm \(I\) (kết quả làm tròn đến hàng phần trăm).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:745275

Phương pháp giải

Suy luận đường đi với mỗi bước ngang hoặc xuống là 1 cách di chuyển.

Giải chi tiết

Gọi \(X\) là biến cố “cả hai người cùng đi qua điểm \(I\)”

Xét hệ trục tọa độ với \(E\left( {0;0} \right),\,\,A\left( {0;8} \right),\,\,B\left( {15;0} \right),\,\,F\left( {15;8} \right),\,\,I\left( {11;5} \right)\)

Để đi từ \(A\) đến \(B\) theo đường ngắn nhất thì người thứ nhất cần di chuyển 15 bước ngang và 8 bước xuống

Số cách di chuyển từ \(A\) đến \(B\) là số cách sắp xếp 15 bước ngang và 8 bước xuống và bằng \(C_{23}^8\)

Tương tự có \(C_{23}^8\) cách để người thứ hai di chuyển từ \(E\) đến \(F\)

Như vậy không gian mẫu \(\left| \Omega \right| = {\left( {C_{23}^8} \right)^2}\)

Người thứ nhất di chuyển từ \(A\left( {0;8} \right)\) đến \(I\left( {11;5} \right)\) cần 11 bước ngang và 3 bước xuống

Người thứ nhất di chuyển từ \(I\left( {11;5} \right)\) đến \(B\left( {15;0} \right)\) cần 4 bước ngang và 5 bước xuống

Như vậy số cách di chuyển của người thứ nhất từ \(A \to I \to B\) là \(C_{14}^3.C_9^4\)

Tương tự số cách di chuyển của người thứ hai từ \(E \to I \to F\) là \(C_{16}^5.C_7^3\)

Như vậy \(\left| X \right| = C_{14}^3.C_9^4.C_{16}^5.C_7^3\)

Vậy xác suất để cả hai người cùng đi qua \(I\) là \(P\left( X \right) = \dfrac{{\left| X \right|}}{{\left| \Omega \right|}} = \dfrac{{C_{14}^3.C_9^4.C_{16}^5.C_7^3}}{{{{\left( {C_{23}^8} \right)}^2}}} \approx 0,029\)

Đáp án: \(0,03\)

Đáp án cần điền là: 0,03

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.