Đề thi thử đại học môn Toán lần 4 năm 2014

Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 1131

Click vào đề thi  

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Giải phương trình: 

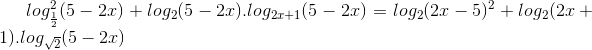
log^{2}_{\frac{1}{2}}(5-2x)+log_{2}(5-2x).log_{2x+1}(5-2x)=log_{2}(2x-5)^{2}+log_{2}(2x+1).log_{\sqrt{2}}(5-2x)

Câu 2: Trong mặt phẳng với hệ toạ độ Oxy cho elip (E): 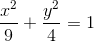\frac{x^{2}}{9}+\frac{y^{2}}{4}=1 và hai điểm A(3;-2), B(-3;2). Tìm trên (E) điểm C có hoành độ và tung độ dương sao cho tam giác ABC có diện tích lớn nhất.

Câu 3: Tìm số nguyên dương n sao cho thoả mãn: 

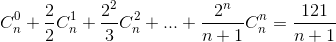
C^{0}_{n}+\frac{2}{2}C^{1}_{n}+\frac{2^{2}}{3}C^{2}_{n}+...+\frac{2^{n}}{n+1}C^{n}_{n}=\frac{121}{n+1}

Câu 4: Cho hàm số x3 – 3mx2 + 3(m2 – 1)x – m3 + m (1)

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) ứng với m=1     (hs tự giải)

2. Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc toạ độ O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.

Câu 5: Giải phương trình: 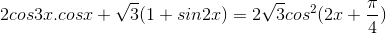\small 2cos3x.cosx+\sqrt{3}(1+sin2x)=2\sqrt{3}cos^{2}(2x+\frac{\pi }{4})

Câu 6: Tính tích phân: 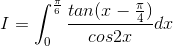I=\int_{0}^{\frac{\pi }{6}}\frac{tan(x-\frac{\pi }{4})}{cos2x}dx

Câu 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là trung điểm của SB và SD; I là giao điểm của SC và mặt phẳng (AMN). Chứng minh SC vuông góc với AI và tính thể tích khối chóp MBAI.

Câu 8: Cho x, y, z là ba số thực dương  thỏa mãn x+y+z = 3

Tìm giá trị nhỏ nhất của biểu thức: P = 3(x2 + y2 + z2) – 2xyz 

Câu 9: Trong không gian với hệ toạ độ Oxyz cho mặt cầu (S): x2 + y2 + z2 – 2x + 6y – 4z – 2 = 0. Viết phương trình mặt phẳng (P) song song với giá của véc tơ \inline \underset{v}{\rightarrow}(1;6;2) vuông góc với mặt phẳng (α) : x+4y+z-11=0 và tiếp xúc với (S)

Câu 10: Trong mặt phẳng với hệ toạ độ Oxy cho điểm C(2;-5 ) và đường thẳng ∆: 3x - 4y + 4 =0. Tìm trên ∆ hai điểm A và B đối xứng nhau qua I(2;\inline \frac{5}{2}) sao cho diện tích tam giác ABC bằng 15.

Câu 11: Tìm hệ số của x4 trong khai triển Niutơn của biểu thức: P = (1+2x+3x2)10

Bạn có đủ giỏi để vượt qua

an.quoc.31149 Phạm Coutinho
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 Phạm Coutinho 9 9 100% 76.1
2 Nguyễn Thanh Tùng 9 9 100% 35.93
3 Mýt Tờ NhÝm 9 9 100% 180.23
4 trần đình bảo 8 8 100% 22.13
5 Optimuz Prime 8 8 100% 25.83
6 nguyen trung khanh 8 9 89% 55.72
7 Nguyễn Minh Sơn 7 9 78% 9.9
8 Do Quang Hung 8 9 89% 57.33
9 trần thị xuân 6 6 100% 119.68
10 Nga Nguyen 7 9 78% 82.32
11 nguyễn nga 7 9 78% 66.62
12 Chung Nguyen Huu 6 8 75% 43.75
13 cafevvn 6 9 67% 52.98
14 Nguyễn Văn A 6 9 67% 29.75
15 Lê Ngọc Văn 6 9 67% 127.43
16 nguyễn thị giang 6 9 67% 23.35
17 nga 7 8 88% 55.7
18 vu 5 8 63% 0.93
19 Trần Gia Bảo 7 9 78% 47.97
20 Đinh Linh 4 6 67% 30.35
21 Thuan Tu Van 5 9 56% 1.15
22 lê văn sang 5 9 56% 10.02
23 Trần Thị Lan 5 9 56% 3.03
24 hoàng xuân chức 4 6 67% 29.32
25 Mot Ngay Moi 5 9 56% 0.52
26 nguyen duc minh 5 9 56% 0.8
27 Nguyễn Thị Hiển 5 9 56% 75.23
28 Tuấn Kiệt Võ Văn 4 6 67% 22.75
29 Quốc Việt 4 4 100% 75.48
30 Như Ngọc 4 4 100% 135.92
31 Quang ObamaObama 4 9 44% 3.58
32 nguyen thi hoa 4 9 44% 5.58
33 Thúy Què 4 9 44% 0.6
34 vo kim thien 3 6 50% 81.53
35 Công Công 4 9 44% 1
36 Mai Hà 4 9 44% 3.35
37 Tuyết Rơi Mùa Hè 3 3 100% 33.65
38 Crystal Song 4 9 44% 67.87
39 Thỏ Ngọc 4 9 44% 6.45
40 Khoảng Cách 3 3 100% 64.15
41 ʚɞLàm Ơnʚɞ 4 9 44% 0.38
42 nguyen long 3 4 75% 48.63
43 nguyễn thảo 4 7 57% 25
44 Nb Văn 3 4 75% 11.48
45 Gstt Nguyen Xuan 1 1 100% 2.22
46 Trung Myth 4 7 57% 5
47 Trịnh Công Anh 1 1 100% 2.42
48 Sóc Nhỏ 2 2 100% 33.68
49 tran gia hoa 2 2 100% 1.98
50 vuonghien 2 2 100% 49.13
51 Nguyễn Minh Sơn 5 9 56% 31.63
52 Nguyễn Văn Trường 2 2 100% 42.03
53 Gaara.PoBc 2 2 100% 26.27
54 RYA 5 9 56% 56.63
55 Bao Viet Huynh Truong 5 9 56% 0.4
56 nguyen phu hien 3 5 60% 54.5
57 Kẹo Trẻ Conn 3 9 33% 9.33
58 Oh Hay 3 9 33% 1.27
59 Nhung Nhí Nhố 3 9 33% 0.68
60 PhongKangkang Ta 3 9 33% 63.48
61 Nguyễn Khánh 3 9 33% 5.63
62 Hận Đời Vô Đối 3 9 33% 0.68
63 vi van thieu 3 9 33% 0.72
64 Lily Phạm 3 9 33% 0.82
65 Trần Duy Khánh 3 9 33% 0.62
66 Thế Ngọc 3 9 33% 1.3
67 Trọng Tiến 3 9 33% 0.6
68 NGUYỄN HOÀNG ANH TUNG 2 3 67% 26.18
69 nguyển trọng hải 3 9 33% 1.13
70 nguyen the tai 3 9 33% 0.43
71 Thanh Chỉ Có Thế 3 9 33% 8.08
72 huynh ngoc quoc 3 9 33% 1.2
73 Dinh Duc 3 9 33% 2.58
74 Nguyễn Ngọc Phương Nam 1 1 100% 0.65
75 nguyen le ly dien 3 7 43% 1.83
76 nguyễn kim phượng 1 1 100% 18.5
77 Bơ Đyk Màk Sốnq 1 1 100% 10.05
78 dang binh 1 1 100% 0.18
79 phamxuandung 1 1 100% 0.13
80 Siêu Nhân Quang 1 1 100% 181.02
81 phamtan 1 1 100% 4.45
82 Tran Huu Vy 1 1 100% 61
83 tuấn anh 1 1 100% 12.95
84 Lê Văn Tiến 1 1 100% 5.47
85 Vĩnh Trường 1 1 100% 3.4
86 nguyennhuthoa 1 1 100% 0.12
87 Thanh Duy Nguyen 1 1 100% 0.5
88 Minh Xmi 1 1 100% 46.88
89 vũ thị hương 1 1 100% 96.15
90 Nguyenthanh Duc 1 1 100% 30.3
91 ngen thi van anh 4 9 44% 1.97
92 Tít Kute 4 9 44% 1.42
93 Lợi Seven 4 9 44% 69.72
94 Chinh Pham 4 9 44% 0.92
95 Chaien Jaian 2 8 25% 3.5
96 Tran Cong Doan 1 2 50% 14.12
97 Hue Dau 4 9 44% 0.6
98 Phạm Gia Bảo 1 2 50% 11.37
99 Nguyễn Đức Nguyện 2 9 22% 0.78
100 Xuân Quân 1 3 33% 11.42
101 Steller Hoàng 0 0 0% 26.32
102 Meoden Mapmap 3 9 33% 8
103 Không Bít Yêu 2 9 22% 5.45
104 caysoi37@gmail.com 0 0 0% 31.48
105 nguyen van tinh 3 9 33% 26.82
106 Trịnh Xuyến Chi 0 0 0% 0.08
107 Đạt_Hunter 0 0 0% 41.45
108 le vuong 0 0 0% 0.47
109 Le lam Quynh Heo 0 0 0% 21.17
110 Thịnh Phan Văn 0 0 0% 0.58
111 Ban Mai Tim 0 0 0% 0.08
112 Vũ văn hùy 0 0 0% 0.03
113 hoang nhu y 0 0 0% 7.37
114 Thach Hoai Kim Nguyen 0 0 0% 1.18
115 pham thanh tuan 0 0 0% 21.78
116 huynh thanh 0 0 0% 0.15
117 Trương Tất Long 0 0 0% 0.08
118 Hồng Liên 0 0 0% 0.03
119 Nguyễn Thanh Sơn 0 0 0% 21.4
120 chu xuân hữu 2 9 22% 4.88
121 Lê Thanh Bình 0 0 0% 2.92
122 lại hoàng thân 0 0 0% 0.05
123 nhoc 0 0 0% 9.45
124 jenny 0 0 0% 1.88
125 Hoàng Chức 0 0 0% 0.65
126 Nghia Nhan Duong 0 0 0% 0.45
127 Thiếu Hiệp 0 0 0% 7.15
128 Cuong Phan 0 0 0% 0.22
129 pham van canh 0 0 0% 8.22
130 Phan Minh Thiện 0 0 0% 0.03
131 nguyen duc ngoc 0 0 0% 0.55
132 chau ho quoc hoa 0 0 0% 0.98
133 Quang Nguyen 3 10 30% 3.55
134 Tuấn Anh 0 0 0% 0.3
135 Manh Asus 0 0 0% 0.45
136 nguyen ngoc duy 0 0 0% 92
137 Jessie Quyen Nguyen 0 0 0% 19.97
138 nguyễn trà oanh 0 0 0% 80.75
139 Trương Anh 0 0 0% 1.65
140 jaybui 0 0 0% 68.95
141 Kha Lê Đình 0 0 0% 0.05
142 Tiểu Tiểu Yêu Ngốc 0 0 0% 0.78
143 đặng đăng khoa 0 0 0% 0.28
144 Trần Tuấn Anh 0 0 0% 0.37
145 Nhi Yến 0 0 0% 1.92
146 Tám Toàn Dê 0 0 0% 9.83
147 Vẫn Như Thế 0 0 0% 3.48
148 Ngô Minh Quân 0 0 0% 1.38
149 thangbkhn 0 0 0% 11.13
150 hung tong 0 0 0% 63.25
151 Nguyễn Thanh Toàn 0 0 0% 0.15
152 Trần Vân Anh 0 0 0% 0.23
153 VÕ ĐẠT 0 0 0% 6.18
154 Heocon Dethuongt 0 0 0% 0.05
155 Su Su 2 9 22% 1.17
156 Hoàng Hiệp 0 0 0% 0.03
157 nguyen sy hieu 0 0 0% 0.18
158 Can Nguyen 3 9 33% 9.42
159 Hong Ha 0 0 0% 4.08
160 Tinh Van Tran 0 0 0% 0.55
161 nguyen thi my 0 0 0% 0.35
162 Duẩn Lê 3 9 33% 1.08
163 nguyen ngan 0 0 0% 0.25
164 do trong anh 0 0 0% 0.05
165 Wise POm 0 0 0% 0.08
166 Phan Mai Linh 2 9 22% 130.23
167 Jun Ngố 0 0 0% 1.38
168 Anh Tuấn Tuấn 0 0 0% 1.22
169 Tấn Ngân Võ 3 9 33% 0.93
170 Ty Gi 1 3 33% 1.05
171 Lê Thị Yến 3 9 33% 88.83
172 Thuan Vuong 0 0 0% 0.05
173 nguyen duc phong 2 7 29% 0.32
174 Đào Thị Sim 3 8 38% 1.53
175 sdgcxbcvvb 0 1 0% 3.95
176 Thales Dương 2 5 40% 181.4
177 Pham Son 2 7 29% 1.32
178 Cỏ May 3 8 38% 10.32
179 huynhlethuy 0 1 0% 4.33
180 le thai ngoc 2 7 29% 2.13
181 Bich Hong Bich 2 7 29% 0.25
182 Huân Trang 2 7 29% 0.37
183 hoang thi trang 0 1 0% 15.8
184 Dương văn định 2 7 29% 2.1
185 Trần Ngọc Trường 0 1 0% 11.45
186 van hung 0 1 0% 9.07
187 Bình Đào Duy 0 1 0% 12.57
188 Nghĩa Vũ 0 1 0% 17.85
189 Nguyễn Duy 2 7 29% 0.23
190 Lương Khắc Tùng 3 8 38% 179.98
191 Huỳnh Quốc Hưởng 0 1 0% 83.35
192 Phương Mai Gee 0 1 0% 0.7
193 lê thị minh trang 0 1 0% 12.28
194 Nguyễn Văn Tuấn 2 7 29% 0.8
195 vothibichphuong 3 9 33% 0.6
196 Tao Deo Can 3 9 33% 5.68
197 Nguyễn Văn Tuấn 3 9 33% 4.48
198 Võ thị thanh loan 3 9 33% 26.35
199 Leonardo Vinci 3 9 33% 3.57
200 hồ phạm my 3 9 33% 1.23
201 Toi Yeu Ls 3 9 33% 0.95
202 nguyen duy son 3 9 33% 0.72
203 abcdefghik 3 9 33% 0.32
204 phan hoàng anh song 3 9 33% 5.5
205 Hụê Đào 3 9 33% 2.4
206 Nguyễn Đình Ngọc 3 9 33% 116.53
207 Vu Khac Manh 3 9 33% 1.83
208 Kieu Anh 3 9 33% 2.08
209 là thị tám 3 9 33% 72.27
210 Nguyễn Hải Triều 0 2 0% 1.05
211 Nguyễn Linh 3 9 33% 1.1
212 thanglq 3 9 33% 1.92
213 Vũ Ngọc Anh 1 6 17% 17.3
214 Vinh Long Nguyen 2 9 22% 2.22
215 Sao Phải Hỏi 1 9 11% 3.93
216 Hoàng Trọng Thành 2 9 22% 3.25
217 Se Se 2 9 22% 1.15
218 Nguyễn văn quang 2 8 25% 5.3
219 Ngoc Pro 2 8 25% 0.68
220 Phu Nguyen 1 7 14% 2.95
221 Lý Cutí 2 9 22% 2.93
222 Nguyễn Văn Hòa 1 8 13% 24.77
223 Dol Baxter 2 9 22% 7.27
224 Tun Tun 2 9 22% 0.88
225 Dola Hoa 2 9 22% 1.33
226 Takkehoa QH 2 9 22% 0.3
227 Linh Tròn 2 9 22% 5.17
228 Hữu Nguyễn 2 9 22% 20.03
229 Độc Cô Cầu Bại 2 9 22% 0.33
230 Kim Tuyến 2 9 22% 1.25
231 Chưa Biết Yêu 2 9 22% 1.97
232 ]v[r.T 2 9 22% 0.63
233 nguyễn văn nhớ 2 9 22% 5.43
234 Tiểu Nha Đầu 2 9 22% 1.42
235 Công Rùa 2 9 22% 139.03
236 Hiền Nguyễn 2 9 22% 1.28
237 nguyen van kha 2 9 22% 0.27
238 Dam minh Hieu 2 9 22% 12.18
239 Chờ Một Ngày Nắng 2 9 22% 4.33
240 Quên Cách Yêu 2 9 22% 2.07
241 Elly Phạm 2 9 22% 0.72
242 nguyenvanmanh 2 9 22% 9.15
243 Thiên Thần Love 1 9 11% 0.72
244 Hoàng Lắm 1 9 11% 1.15
245 Kull Pham 1 9 11% 13.38
246 Tien Nguyen Quoc 1 9 11% 36.88
247 lê nguyễn minh hoàng 1 9 11% 2
248 The Vu 1 9 11% 1.37
249 kiên chí linh 1 9 11% 0.68
250 vo tan ngan 1 9 11% 0.25
251 Ly Biu 1 9 11% 1.98
252 Trương Minh Dũng 1 9 11% 5.43
253 vo van tinh 1 9 11% 1.3
254 Đặng Thị Tiến 1 9 11% 2.8
255 Tập Sống Phũ 1 9 11% 0.65
256 Như Nguyễn 1 9 11% 1.13
257 hIEU bp 1 9 11% 1
258 Dinh Thuy 0 9 0% 11.77
259 Hồng Huệ Nguyễn 0 9 0% 0.57
260 Nam Mai 0 9 0% 0.9
261 Ku Pi 0 9 0% 1.02

Cùng tham gia trao đổi với bạn bè!

Lớp 12