Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 91:
Từ một điểm E ở ngoài đường tròn Tâm O kẻ 2 tiếp tuyến với đường tròn tại A và B .Gọi M là điểm nằm trên đoạn AB (M khác A và B ,MA≠MB).Gọi C và D là 2 điểm trên đường tròn sao cho M là trung điểm của CD .Các tiếp tuyến của đường tròn tại C và D cắt nhau tại F.Chứng minh rằng tam giác OEF là tam giác vuông
Bài 92:
Đường thẳng đi qua điểm H và vuông góc với AO cắt nửa đường tròn (O) tại C. Trên cung BC lấy điểm D bất kỳ (D khác B và C). Tiếp tuyến của nửa đường tròn (O) tại D cắt đường thẳng HC tại E. Gọi I là giao điểm của AD và HC
Câu hỏi số 1:
Chứng minh tứ giác BHID nội tiếp đường tròn
Câu hỏi số 2:
Chứng minh tam giác IED là tam giác cân
Câu hỏi số 3:
Đường thẳng qua và song song với AB cắt BC tại K. Chứng minh tâm đường tròn ngoại tiếp tam giác ICD là trung điểm của đoạn CK
Câu hỏi số 93:
Cho tam giác ABC ,M là trung điểm của BC gọi r,r1,r2 thứ tự là bán kính đường tròn nội tiếp ∆ABC ,∆BM,∆ ACM và BC = a.Chứng minh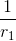 
+
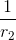≥ 2(
+
)
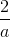Bài 94:
Cho nửa đường tròn tâm O bán kính AB, trên nửa đường tròn lấy điểm C (C khác A và B). Trên cung BC lấy điểm D (D khác B và C). Vẽ đường thẳng d vuông góc với AB tại B. Các đường thẳng AC và AD cắt d lần lượt tại E và F
Câu hỏi số 1:
Chứng minh tứ giác CDFE nội tiếp đường tròn
Câu hỏi số 2:
Gọi I là trung điểm của BF. Chứng minh ID là tiếp tuyến của nửa đường tròn đã cho
Câu hỏi số 3:
Đường thẳng CD cắt d tại K, tia phân giác của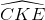 
cắt AE và AF lần lượt tại M và N. Chứng minh tam giác AMN là tam giác cân
Bài 95:
Cho tam giác nhọn nội tiếp đường tròn (O). AD,BE,CF là ba đường cao (D∈BC,E∈CA,F∈AB). Đường thẳng EF cắt BC tại G, đường thẳng AG cắt lại đường tròn (O) tại điểm M.
Câu hỏi số 1:
Chứng minh rằng bốn điểm A,M,E,F cùng nằm trên một đường tròn.
Câu hỏi số 2:
Gọi N là trung điểm cạnh BC và H là trực tâm tam giác ABC. Chứng minh rằng GH⊥AN
Bài 96:
Cho đường tròn tâm O đường kính A = 2R. Gọi M là một điểm nằm trên đường tròn (O) sao cho AM = R; C là một điểm tùy ý trên đoạn OB (C khác B). Đường thẳng qua C và vuông góc với AB lần lượt cắt đường thẳng MA, MB tại K và H
Câu hỏi số 1:
Chứng minh tứ giác AMHC nội tiếp
Câu hỏi số 2:
Tính độ dài đoạn BM và diện tích tam giác MAB theo R
Câu hỏi số 3:
Tiếp tuyến của đường tròn (O) tại M cắt CK tại I. Chứng minh tam giác MIH đều
Câu hỏi số 4:
Các đường thẳng KB và MC cắt đường tròn (O) lần lượt tại E và F. Chứng minh EF song song với KC
Bài 97:
Cho (O;R) đường kính EF. Bán kính OI vuông góc với EF, gọi J là điểm bất kỳ trên Cung nhỏ EI( J khác E và I), FJ cắt EI tại L; Kẻ LS vuông góc với EF (S thuộc EF)
Câu hỏi số 1:
Chứng minh tứ giác IFSL nội tiếp
Câu hỏi số 2:
Trên đoạn thẳng FJ lấy điểm N sao cho FN = EJ. Chứng minh rằng tam giác IJN vuông cân
Câu hỏi số 3:
Gọi (d) à tiếp tuyến tại E, Lấy điểm D là điểm nằm trên (d) sao cho hai điểm D và I cùng nằm trên cùng một nửa mặt phẳng bờ là đường thẳng FE và ED.JF = JE.OF Chứng minh rằng đường thẳng FD đi qua trung điểm của đoạn LS.
Bài 98:
Cho đường tròn tâm O đường kính AB. M là điểm chính giữa cùa cung AB. K là một điêm bất kỳ trên cung nhỏ BM. Gọi H là chân đường vuông góc của M xuống AK
Câu hỏi số 1:
Chứng minh rằng AOHM là tứ giác nội tiếp
Câu hỏi số 2:
Tam giác MHK là tam giác gì? Vì sao?
Câu hỏi số 3:
Chứng minh OH là tia phân giác của góc MOK
Câu hỏi số 4:
Gọi p là hình chiếu vuông góc của K lên AB. Xác định vị trí cùa K để chu vi tam giác OPK lớn nhất
Bài 99:
Cho đường tròn tâm O, bán kính R và dây cung BC cố định có độ dài BC = R√3. A là một điểm duy nhất thay đổi trên cung lớn BC. Gọi E là điểm đối xứng của B qua AC và F là điểm đối xứng của C qua AB. Các đường tròn ngoại tiếp các tam giác ABE và ACF cắt nhau tại K ( K ≠ A )
Câu hỏi số 1:
Chứng minh K luôn thuộc một đường tròn cố định
Câu hỏi số 2:
Xác định vị trí của điểm A để tam giác KBC có diện tích lớn nhất là tìm giá trị lớn nhất đó theo R
Câu hỏi số 3:
Gọi H là giao điểm của BE và CF. chứng minh ∆ ABH ∽∆ AKC và đường thẳng AK luôn đi qua một điểm cố định
Bài 100:
Cho hình chữ nhật ABCD có tâm O, cạnh AB = 3a và góc ABD bằng 300. Gọi G là trọng tâm tam giác AOD, AG cắt CD tại E
Câu hỏi số 1:
Chứng minh tứ giác AOED nội tiếp trong một đường tròn
Câu hỏi số 2:
Cho DG cắt AB tại F. Tính diện tích tứ giác AFOE
Câu hỏi số 3:
Đường tròn tâm J nội tiếp tam giác BCD tiếp xúc với BD, CD lần lượt tại I, K. Gọi H là giao điểm của IK và AC. Tính góc IOJ và độ dài đoạn HE
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
