Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 261:
Cho (O;R); BC = R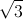
là một dây cung cố định của (O;R). A là điểm trên cung lớn BC. Kẻ BD, CE là các đường cao của tam giác ABC, chúng cắt nhau tại H.
Câu hỏi số 1:
Chứng minh tứ giác BEDC nội tiếp.
Câu hỏi số 2:
CH.CE + BH.BD không đổi khi điểm A thay đổi trên cung lớn BC.
Câu hỏi số 3:
Cho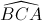 
= 
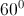, quay tam giác vuông BDC một vòng quanh cạnh BD. Tính diện tích xung quanh và thể tích hình tạo tạo thành.
Bài 262:
Cho đường tròn tâm O đường kính AB=2R và C là trung điểm của OA. Qua C kẻ dây cung MN vuông góc với OA. Gọi K là điểm tùy ý trên cung nhỏ BM,H là giao điểm của AK và MN.
Câu hỏi số 1:
Chứng minh tứ giác BCHK nội tiếp.
Câu hỏi số 2:
Tính tích AH.AK theo R.
Câu hỏi số 3:
Chứng minh tam giác MBN là tam giác đều.
Câu hỏi số 4:
Xác định vị trí điểm K trên cung nhỏ BM để KM+KN+KB đạt giá trị lớn nhất. Tính giá trị lớn nhất đó theo R.
Bài 263:
Cho đường tròn tâm O; bàn kính R và đường tròn tâm O', bán kính R'(R>R') cắt nhau tại hai điểm A và B. Đường thẳng AB cắt B. Vẽ tiếp tuyến chung MN của 2 đường tròn. Đường thẳng AB cắt MN tại I(B nằm giữa A và I).
Câu hỏi số 1:
Chứng minh rằng: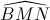 
= 
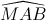
Câu hỏi số 2:
Chứng minh rằng: IN2 = IA.IB
Câu hỏi số 3:
Đường thẳng MA cắt cắt đường thẳng NB tại Q, đường thẳng NA cắt đường thẳng MB tại P. Chứng minh rằng MN//QP.
Bài 264:
Cho đường tròn (O) và điểm M nằm ngoài đường tròn (O). Qua điểm M kẻ 2 tiếp tuyến MA, MB đến đường tròn (O) với A, B là các tiếp điểm. MPQ là cát tuyến không đi qua tâm O, P nằm giữa M và Q. Qua P kẻ đường thẳng vuông góc với OA cắt AB, AQ tương ứng tại R, S. Gọi trung điểm của đoạn PQ là N
Câu hỏi số 1:
Chứng minh rằng 5 điểm M,A,N,O,B cùng thuộc một đường tròn. Chỉ rõ bán kính của đường tròn đó.
Câu hỏi số 2:
Chứng minh rằng: RP = RS
Bài 265:
Cho đường tròn (O; R) có đường kính AB , kẻ tiếp tuyến Ax và lấy điểm P (AP > R).Từ P kẻ tia PM tiếp xúc với (O) tại M.
Câu hỏi số 1:
Tứ giác OBMP là hình gì? Tại sao?
Câu hỏi số 2:
Cho AP = R√3. Chứng minh rằng ∆PAM có trực tâm H nằm trên (O; R).
Câu hỏi số 3:
Chứng minh rằng : Khi P di động trên tia Ax (AP > R) thì trực tâm H của ∆PAM chạy trên cung cố định.
Bài 266:
Cho đường tròn tâm O, đường kính BC và một điểm A trên nửa đường tròn (A khác B và C). Hạ AH vuông góc với BC ( H thuộc BC). Trên nửa mặt phẳng bờ BC chứa A, dựng hai nửa đường tròn đường kính HB và HC, chúng lần lượt cắt AB và AC tại E và F.
Câu hỏi số 1:
Chứng minh rằng AE.AB = AF.AC
Câu hỏi số 2:
Chứng minh rằng EF là tiếp tuyến chung của hai nửa đường tròn đường kính HB và HC.
Bài 267:
Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Câu hỏi số 1:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
Câu hỏi số 2:
Chứng minh DM.CE=DE.CM
Câu hỏi số 3:
Tính AC và BD biết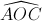 
= 
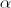. Chứng tỏ tích AC.BD không phụ thuộc vào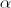
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
