Tổ hợp - Xác suất
Chuyên đề này giới thiệu cho các bạn một số dạng bài tập về công thức tổ hợp, xác suất.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 111:
Khai triển và rút gọn biểu thức: P(x) = 1 - x - 2(1 - x2) + …+ n(1 – x)n , n ∈ N* thu được đa thức P(x) = a0 + a1x + … + anxn . Tính hệ số a8 biết n thỏa mãn: 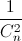 +
+ 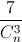 =
= 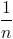
Câu hỏi số 112:
Hai bạn An và Bình thi đấu với nhau một trận bóng bàn. Họ quy ước chơi với nhau nhiều nhất 5 séc, ai thắng trước 3 séc là người thắng cuộc và trận đấu kết thúc.Tính xác xuất để trận đấu kết thúc sau séc thứ tư, biết rằng xác suất An thắng trong mỗi séc là 0,4 và séc nào cũng có người thắng
Câu hỏi số 113:
Viết ngẫu nhiên một số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau lên bảng. Tính xác xuất để số vừa viết thỏa mãn trong số đó mỗi chữ số đều lớn hơn chữ số đứng trước nó
Câu hỏi số 114:
Cho khai triển ( x + 1)n = 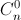 xn +
xn + 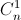 xn – 1 +
xn – 1 + 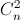 xn – 2 + …+
xn – 2 + …+ 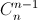 x +
x + 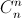 .Biết rằng trong khai triển có ba hệ số liên tiếp tỉ lệ với 2:15:70. Tìm n. Tính tổng tất cả các hệ số của các lũy thừa bậc lẻ của x.
.Biết rằng trong khai triển có ba hệ số liên tiếp tỉ lệ với 2:15:70. Tìm n. Tính tổng tất cả các hệ số của các lũy thừa bậc lẻ của x.
Câu hỏi số 115:
Tinh P = 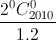 -
- 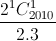 +
+ 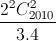 -
- 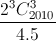 +...+
+...+ 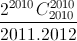
Câu hỏi số 116:
Chọn ngẫu nhiên một số tự nhiên có 5 chữ số. Tính xác suất để số đó không có chữ số 1 hoặc không có chữ số 5.
Câu hỏi số 117:
Tìm hệ số lớn nhất trong khai triển thành đa thức của (2x + 1)n biết tổng các hệ số của nó là 59049.
Câu hỏi số 118:
Cho P(x) = ( 1+ 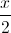 )20, tìm hệ số lớn nhất trong khai triển.
)20, tìm hệ số lớn nhất trong khai triển.
Câu hỏi số 119:
Có tất cả bao nhiêu số tự nhiên có bốn chữ số phân biệt lớn hơn 2012 sao cho chữ số hàng nghìn không lớn hơn chữ số hàng đơn vị.
Câu hỏi số 120:
Từ các số 0,1,2,3,4,5,6 có thể lập thành được bao nhiêu số tự nhiên khác nhau mà ở mỗi số này các chữ số đều khác nhau và có mặt chữ số 4.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









