Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Tổ hợp - Xác suất
Chuyên đề này giới thiệu cho các bạn một số dạng bài tập về công thức tổ hợp, xác suất.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 131:
Viết ngẫu nhiên một số tự nhiên gồm 5 chữ số phân biệt lên bảng. Tính xác suất để trong số đó có mặt chữ số 1 và chữ số 3.
Câu hỏi số 132:
Khai triển và rút gọn biểu thức 1 – x + 2(1 – x)2 +…+n( 1 –x)n thu được đa thức P(x) = a0 + a1x + …+anxn. Tìm hệ số a8 biết rằng n là số nguyên dương thỏa mãn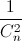 
+ 
= 
. ( 
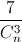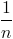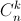là số tổ hợp chập k của n phần tử).
Câu hỏi số 133:
Tìm số hạng không chứa x trong khai triển theo nhị thức Niutơn biểu thức A = (x√x +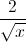 
)n, (x > 0), trong đó n là số nguyên dương thỏa mãn 2n + 
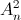+ 3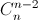
= 
+ 
( 
; 
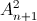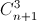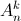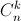lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
Câu hỏi số 134:
Cho khai triển (2 –![\sqrt[3]{3}](http://images.tuyensinh247.com/picture/learning/exam/2013/1115/2782_23152_1.gif)
x)2n = a0 + a1x + ….+ a2nx2n.Tính hệ số a9, biết rằng số tự nhiên n thỏa mãn hệ thức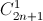 
+ 
+ 
+...+ 
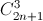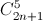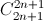= 4096 ( 
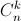là số tổ hợp chập k của n phần tử ).
Câu hỏi số 135:
Trong kì thi tuyển sinh đại học, bạn An dự thi hai môn thi trắc nghiệm Vật lí và Hóa học, đề thi của mỗi môn gồm 50 câu hỏi, mỗi câu có 4 phương án lựa chọn, trả lời đúng mỗi câu được 0,2 điểm. Mỗi môn thi An đều trả lời hết các câu hỏi và chắc chắn đúng 45 câu; 5 câu còn lại An chọn ngẫu nhiên. Tính xác suất để tổng số điểm 2 môn thi của An không dưới 19 điểm.
Câu hỏi số 136:
Có bao nhiêu số tự nhiên chẵn gồm bốn chữ số sao cho trong số đó mỗi chữ số lớn hơn các chữ số đứng trước nó
Câu hỏi số 137:
An và Bình thi đấu với nhau một trận bóng bàn, người nào thắng trước 3 séc thì thắng trận. Xác suất An thắng mỗi séc là 0,4 (không có hòa). Tính xác suất An thắng trận.
Câu hỏi số 138:
Một nhóm 10 học sinh gồm 6 nam trong đó có Quang và 4 nữ trong đó có Huyền đươc xếp ngồi vào 10 cái ghế trên một hàng ngang để dự Lễ tổng kết năm học. Có bao nhiêu cách sắp xếp thỏa mãn giữa 2 bạn nữ gần nhau có 2 bạn nam, đồng thơi Quang không ngồi cạnh Huyền.
Câu hỏi số 139:
Một tổ gồm 10 học sinh trong đó có 3 học sinh không thuộc bài. Cô giáo kiểm tra bài cũ bằng cách gọi lần lượt từng học sinh cho đến khi có học sinh thuộc bài trả lời được câu hỏi thì dừng lại. Gọi X là số học sinh được hỏi bài cũ, lập bảng phân bố xác suất của X.
Câu hỏi số 140:
Người ta sử dụng 5 cuốn sách tiếng Anh, 6 cuốn tiếng Pháp, 7 cuốn tiếng Nhật (các cuốn sách cùng loại giống nhau) để làm giải thưởng cho 9 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 9 học sinh trên chó hai bạn Lan và Nam. Tìm sác xuất để hai bạn Lan và Nam có giải thưởng giống nhau.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
