Hàm số và các bài toán liên quan
Chuyên đề này giúp học sinh giải các bài tập về hàm số và các bài toán liên quan.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 1:
Cho hàm số y = 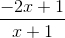 (1).
(1).
a, Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) (HS tự làm ).
b, Tìm m để đường thẳng d: y = -x + m cắt (C) tại 2 điểm A, B thỏa mãn AB = 2√2
Câu hỏi số 2:
Cho hàm số y = −x3 + (2m + 1)x2 − 2 (1), với m là tham số thực
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1. (HS tự làm)
2. Tìm m để đường thẳng d: y = 2mx −2 cắt đồ thị hàm số (1) tại ba điểm phân biệt A(0;−2), B(1;2m − 2), C sao cho AC = 2.AB
Câu hỏi số 3:
Cho hàm số y = 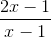 có đồ thị (C)
có đồ thị (C)
a) Khảo sát vẽ đồ thị hàm số (C). ( HS tự làm)
b) Viết phương trình tiếp tuyến với đồ thị (C). Biết khoảng cách từ điểm I(1;2) đến tiếp tuyến đó bằng √2
Câu hỏi số 4:
Cho hàm số y = x3+ -3mx2+ 3(m2-1)x -m3+ 5m (1), trong đó m là tham số.
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số (1) khi m=1.
b) Chứng minh rằng với mọi m, đồ thị hàm số (1) luôn có hai điểm cực trị A, B, đồng thời trung điểm I của AB chạy trên một đường thẳng cố định.
Câu hỏi số 5:
Cho hàm số y = x3 -3mx2+3(m2-1)x -m3+5m (1), trong đó m là tham số.
a, Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số (1) khi m=1.
b, Chứng minh rằng với mọi m, đồ thị hàm số (1) luôn có hai điểm cực trị A, B và độ dài của đoạn thẳng AB không phụ thuộc vào m.
Câu hỏi số 6:
Cho hàm số y 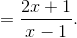 có đồ thị là (C)
có đồ thị là (C)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự giải)
Tìm các giá trị m để đường thẳng y = -3x + m cắt (C) tại A và B sao cho trọng tâm của tam giác OAB thuộc đường thẳng x – 2y – 2 = 0 (O là gốc tọa độ ).
Câu hỏi số 7:
Cho hàm số y =−x3 +3x2 +3m(m+ 2) x+1 (1), với m là tham số thực.
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m= 0.
b) Tìm m để đồ thị hàm số (1) có hai điểm cực trị đối xứng nhau qua điểm I(1;3) .
Câu hỏi số 8:
Cho hàm số y=−x4 −2mx2 +m2 +m (1) , với m là tham số thực.
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m=−2.
b) Tìm tất cả các giá trị của m để đồ thị hàm số (1) cắt trục hoành tại bốn điểm phân biệt.
Câu hỏi số 9:
Cho hàm số: 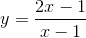
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. (hs tự giải)
2) Viết phương trình tiếp tuyến của (C), biết khoảng cách từ điểm I(1;2) đến tiếp tuyến bằng √2.
Câu hỏi số 10:
Cho hàm số: 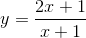
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho. (hs tự giải)
b) Tìm m ∈ R để đường thẳng y=x+m cắt đồ thi (C) tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại O. (với O là gốc toạ độ).
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









