Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 51:
Cho đường tròn (O; R) với dây cung BC cố định (BC < 2R) và điểm A trên cung lớn BC (A không trùng B, C). Gọi H là trực tâm của tam giác ABC và A', B', C' lần lượt là hình chiếu vuông góc của A, B, C lên các cạnh BC, CA, AB.
Câu hỏi số 1:
Chứng minh OA ┴ B'C'
Câu hỏi số 2:
Chứng minh: BA.BH = 2R.BA'. Từ đó suy ra tổng: BA.BH + CA.CH không đổi.
Bài 52:
Cho đường tròn (O) và đường thẳng d cắt (O) tại hai điểm C, D. Từ điểm M tùy ý trên d kẻ các tiếp tuyến MA, MB với (O) (A, B là các tiếp điểm). Gọi I là trung điểm CD.
Câu hỏi số 1:
Chứng minh tứ giác MAIB nội tiếp
Câu hỏi số 2:
Giả sử MO và AB cắt nhau tại H. Chứng minh H thuộc đường tròn ngoại tiếp tam giác COD.
Câu hỏi số 3:
Chứng minh AB đi qua I điểm cố định khi M thay đổi trên d.
Câu hỏi số 4:
Chứng minh :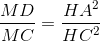
Bài 53:
Cho hai đường tròn (O) và (O') cắt nhau tại A, B . Kẻ tiếp tuyến chung CD (C, D là tiếp điểm và C thuộc (O), D thuộc (O')). Qua B kẻ cát tuyến song song với CD cắt (O) tại E cắt (O') tại F. Gọi M, N theo thứ tự là giao điểm của DA và CA với EF. Gọi I là giao điểm của EC với FD. Chứng minh rằng:
Câu hỏi số 1:
CD là trung trực của đoạn BI.
Câu hỏi số 2:
Tam giác MIN cân.
Bài 54:
Cho đường tròn (O) và điểm M nằm ngoài đường tròn (O). Từ điểm M kẻ hai tiếp tuyến MA, MC (A,C là các tiếp điểm) tới đường tròn (O). Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD không đi qua (O). Gọi H là giao điểm của OM và AC. Từ C kẻ đường thẳng song song với BD cắt đường tròn (O) tại E (E khác C). Gọi K là giao điểm của AE và BD.
Câu hỏi số 1:
Chứng minh tứ giác OAMC nội tiếp.
Câu hỏi số 2:
Chứng minh K là trung điểm của BD.
Câu hỏi số 3:
Chứng minh AC là phân giác của góc BHD.
Bài 55:
Cho đoạn thẳng BC có M là trung điểm. Gọi H là một điểm của đoạn thẳng BM (H khác các điểm B và M). Trên đường thẳng vuông góc với BC tại H lấy điểm A sao cho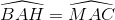 
. Đường tròn tâm A bán kính AB cắt đoạn thẳng BC tại điểm thứ hai ở D và cắt đoạn thẳng AC tại E. Gọi P là giao điểm của AM và EB.
Câu hỏi số 1:
Đặt AB = r. Tính tích DH.AM theo r.
Câu hỏi số 2:
Gọi h1, h2, h3 lần lượt là khoảng cách từ điểm P đến các đường thẳng BC, CA, AB. Chứng minh rằng: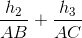 
< 
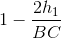
Câu hỏi số 3:
Gọi Q là giao điểm thứ hai của hai đường tròn ngoại tiếp hai tam giác APE và BPM. Chứng minh rằng tứ giác BCEQ là tứ giác nội tiếp.
Bài 56:
Cho đường tròn (O) và điểm A nằm bên ngoài (O). Kẻ hai tiếp tuyến AM, AN với đường tròn (O). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm B và C (AB < AC, d không đi qua tâm O).
Câu hỏi số 1:
Chứng minh tứ giác AMON nội tiếp.
Câu hỏi số 2:
Chứng minh : AN2 = AB.AC. Tính độ dài đoạn thẳng BC khi AB = 4 cm, AN = 6 cm.
Câu hỏi số 3:
Gọi I là trung điểm BC. Đường thẳng NI cắt đường tròn (O) tại điểm thứ hai T. Chứng minh MT // AC.
Câu hỏi số 4:
Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại K. Chứng minh K thuộc một đường thẳng cố định khi d thay đổi và thỏa mãn điều kiện bài toán.
Bài 57:
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có trực tâm H. Gọi P là điểm nằm trên đường tròn ngoại tiếp tam giác HBC (P khác B, C và H) và nằm trong tam giác ABC. PB cắt (O) tại M khác B, PC cắt (O) tại N khác C. BM cắt AC tại E, CN cắt AB tại F. Đường tròn ngoại tiếp tam giác AME và đường tròn ngoại tiếp tam giác ANF cắt nhau tại Q khác A.
Câu hỏi số 1:
Chứng minh rằng ba điểm: M, N, Q thẳng hàng.
Câu hỏi số 2:
Giả sử AP là phân giác góc MAN. Chứng minh rằng khi đó PQ đi qua trung điểm của BC.
Bài 58:
Cho ∆ ABC nhọn nội tiếp đường tròn (O) với AB < AC. Đường phân giác của 
cắt (O) tại D khác A. Gọi M là trung điểm của AD cà E là điểm đối xứng với D qua O. Giả dụ (ABM) cắt AC tại F.
Câu hỏi số 1:
Chứng minh: ∆ BDM ~ ∆ BCF
Câu hỏi số 2:
Chứng minh: EF vuông góc với AC.
Bài 59:
Cho tam giác ABC nhọn nội tiếp đường tròn (O), AB < AC. Các tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại E; AE cắt đường tròn (O) tại D (khác điểm A). Kẻ đường thẳng (d) qua điểm E và song song với tiếp tuyến tại A của đường tròn (O), đường thẳng (d) cắt các đường thẳng AB, AC lần lượt tại P và Q. Gọi M là trung điểm của đoạn thẳng BC. Đường thẳng AM cắt đường tròn (O) tại N (khác điểm A).
Câu hỏi số 1:
Chứng minh rằng: EB2 = ED.EA và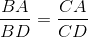 
Câu hỏi số 2:
Chứng minh các đường tròn ngoại tiếp của ba tam giác ABC, EBP, ECQ cùng đi qua một điểm.
Câu hỏi số 3:
Chứng minh E là tâm đường tròn ngoại tiếp của tứ giác BCQP.
Câu hỏi số 4:
Chứng minh tứ giác BCND là hình thang cân.
Bài 60:
Cho tam giác ABC nội tiếp đường tròn (O), bán kính R, BC = a, với a và R là các số thực dương. Gọi I là trung điểm của cạnh BC. Các góc 
, 
, 
đều là góc nhọn.
Câu hỏi số 1:
Tính OI theo a và R.
Câu hỏi số 2:
Lấy điểm D thuộc đoạn AI, với D khác A, D khác I. Vẽ đường thẳng qua D song song với BC cắt cạnh AB tại điểm E. Gọi F là giao điểm của tia CD và đường tròn (O), với F khác C. Chứng minh tứ giác ADEF là tứ giác nội tiếp đường tròn.
Câu hỏi số 3:
Gọi J là giao điểm của tia AI và đường tròn (O), với J khác A. Chứng minh: AB.BJ = AC.CI
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
