Tổ hợp - Xác suất
Chuyên đề này giới thiệu cho các bạn một số dạng bài tập về công thức tổ hợp, xác suất.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 21:
Tính tổng 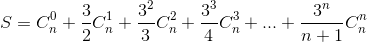
Câu hỏi số 22:
Cho khai triển Niutow ![\left ( 2^{log_{2}^{\sqrt[3]{9^{x-1}+7}}} +2^{-\frac{1}{5}log_{2}(3^{x-1}+1)}\right )^{8}](http://images.tuyensinh247.com/picture/learning/exam/2014/0408/43471_577445_1.gif) . Hãy tìm các giá trị của x ∈ R, biết rằng số hạng thứ 6 từ trái sang phải trong khai triển này là 224.
. Hãy tìm các giá trị của x ∈ R, biết rằng số hạng thứ 6 từ trái sang phải trong khai triển này là 224.
Câu hỏi số 23:
Cho tập E = {1, 2, 3, 4, 5}. Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập E. Tính xác suất để trong hai số đó có đúng một số có chữ số 5 .
Câu hỏi số 24:
Tìm hệ số của x7 trong khai triển nhị thức Niu-tơn của (x2 - 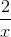 )n, biết rằng n là số nguyên dương thỏa mãn 4
)n, biết rằng n là số nguyên dương thỏa mãn 4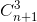 + 2
+ 2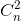 =
=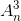 .
.
Câu hỏi số 25:
Cho khai triển P(x) = (x3 + 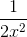 )n ta được
)n ta được
P(x) = a0x3n + a1x3n – 5 + a2x3n – 10 +......
Biết rằng 3 hệ số đầu a0, a1, a2 lập thành một cấp số cộng. Tính n và hệ số của số hạng chứa x4 trong khai triển trên.
Câu hỏi số 26:
Một trường THPT có 18 học sinh giỏi toàn diện trong đó có 7 học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn 8 học sinh trong tổng số 18 học sinh trên đi dự trại hè sao cho mỗi khối có ít nhất 1 học sinh.
Câu hỏi số 27:
Chứng minh rằng với mọi số nguyên dương n ta luôn có:
12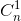 + 22
+ 22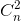 + ... + n2
+ ... + n2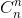 = n(n + 1).2n-2
= n(n + 1).2n-2
Câu hỏi số 28:
Người ta sử dụng 5 cuốn sách Toán, 6 cuốn sách Vật lí, 7 cuốn sách Hóa học ( các cuốn sách cùng loại giống nhau ) để làm giải thưởng cho 9 học sinh, mỗi học sinh được hai cuốn sách khác loại. Trong số 9 học sinh trên có hai bạn Ngọc và Thảo. Tìm xác suất để hai bạn Ngọc và Thảo có giải thưởng giống nhau.
Câu hỏi số 29:
Với n là số nguyên dương, chứng minh hệ thức
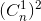 +2
+2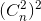 +3
+3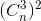 +...+(n-1)(
+...+(n-1)(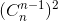 +n
+n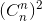 =
=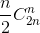
Câu hỏi số 30:
Tìm số hạng không chứa x trong khai triển ![\left ( \sqrt{x}+\frac{1}{2\sqrt[4]{x}}\right )^{n}](http://images.tuyensinh247.com/picture/learning/exam/2014/0404/42549_763038_1.gif) , biết rằng tổng các hệ số của khai triển (a + b)n bằng 4096 (n ∈ N*, x > 0).
, biết rằng tổng các hệ số của khai triển (a + b)n bằng 4096 (n ∈ N*, x > 0).
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









