Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 51:
Cho đường tròn (O), từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB và AC (B và C là hai tiếp điểm). Gọi M là giao điểm của OA và BC, D là một điểm nằm trên đường tròn (O) sao cho D không nằm trên đường thẳng OA, kẻ dây cung DE đi qua M. Chứng minh tứ giác ADOE nội tiếp.
Bài 52:
Cho đường tròn tâm O đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ hai tiếp tuyến AM, AN với đường tròn (O) (M, N là hai tiếp điểm). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
Câu hỏi số 1:
Năm điểm A, O, M, N, F cùng nằm trên một đường tròn
Câu hỏi số 2:
Ba điểm M, N, H thẳng hàng
Câu hỏi số 3:
HA.HF=R2 – OH2
Bài 53:
Cho tam giác ABC không có góc tù (AB < AC), nôi tiếp đường tròn (O;R) (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đừng thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I
Câu hỏi số 1:
Chứng minh rằng 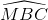 =
= 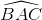 . Từ đó suy ra tứ giác MBIC nội tiếp
. Từ đó suy ra tứ giác MBIC nội tiếp
Câu hỏi số 2:
Chứng minh rằng FI.FM = FD.FE
Câu hỏi số 3:
Đường thẳng OI cắt (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt (O) tại T (T khác Q). Chứng mnh ba điểm P, T, M thẳng hàng
Câu hỏi số 4:
Tìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất
Bài 54:
Cho tam giác ABC nội tiếp đường tròn đường kính AB với AC < BC và đườn cao CH. Trên cung nhỏ BC lấy điểm M (M khác B và C), gọi E là giao điểm của CH và AM
Câu hỏi số 1:
Chứng minh tứ giác EHBM là tứ giác nội tiếp
Câu hỏi số 2:
Chứng minh AC2 = AH.AB và AC.EC = AE.CM
Câu hỏi số 3:
Chứng minh AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CEM. Xác định vị trí điểm M để khoảng cách từ H đến tâm đường tròn ngoại tiếp tam giác CEM là ngắn nhất
Bài 55:
Cho tam giác ABC (AB < AC) có ba góc đều nhọn và nội tiếp đường tròn tâm O, bán kính R. Vẽ đường kính AD và đường cao AH (H ∈ BC). Từ B và C kẻ BI và CK cùng vuông góc với AD cắt AD lần lượt tại I và K.
Câu hỏi số 1:
Chứng minh tứ giác ABHI và tứ giác AHKC nội tiếp.
Câu hỏi số 2:
Chứng mính IH // CD
Câu hỏi số 3:
Chứng minh ∆IHK và ∆BAC đồng dạng
Câu hỏi số 4:
Cho 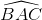 = 600. Tính diện tích của hình giới hạn bởi dây BC và cung đường tròn tâm O theo R
= 600. Tính diện tích của hình giới hạn bởi dây BC và cung đường tròn tâm O theo R
Bài 56:
Cho đường tròn tâm O đường kính AB. Trên đường tròn lấy điểm C sao cho AC < BC (C ≠ A). Tiếp tuyến Bx của đường tròn (O) cắt đường trung trực BC tại D. Gọi F là giao điểm của DO và BC
Câu hỏi số 1:
Chứng minh CD là tiếp tuyến của đường tròn (O)
Câu hỏi số 2:
Gọi E là giao điểm của AD với đường tròn (O) (với E ≠ A) Chứng minh DE.DA = DC2 = DF.DO
Câu hỏi số 3:
Gọi H là hình chiếu của C trên AB, I là giao điểm của AD và CH. Chứng minh I là trung điểm của CH
Bài 57:
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O, bán kính R. Ba đường cao AD, BE và CK của tam giác ABC cắt nhau tại H sao cho AH = R. Gọi M, N lần lượt là trung điểm của cạnh AB và AC
Câu hỏi số 1:
Chứng minh tứ giác AMON nội tiếp được đường tròn
Câu hỏi số 2:
Tính diện tích của hình tròn ngoại tiếp tứ giác AMON theo R
Câu hỏi số 3:
Tính số đo của góc BAC
Bài 58:
Cho đường tròn (O) bán kính R = 3cm và một điểm I nằm ngoài đường tròn , biết rằng OI = 4cm. Từ 1 kẻ hai tiếp tuyến IA và IB với đường tròn (A, B là tiếp điểm)
Câu hỏi số 1:
Chứng minh tứ giác OAIB nội tiếp
Câu hỏi số 2:
Từ I kẻ đường thẳng vuông góc với OI cắt tia OA tại O'. Tính OO' và diện tích tam giác IOO'
Câu hỏi số 3:
Từ O' kẻ O'C vuông óc BI cắt đường thẳng BI tại C. Chứng minh O'I là đường phân giác của 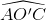
Bài 59:
Cho đường tròn (O) bán kính R và một điểm A sao cho OA = 3R. Qua A kẻ 2 tiếp tuyến AP và AQ với đường tròn (O;R) (P, Q là 2 tiếp điểm). Lấy M thuộc đường tròn (O;R) sao cho PM song song với AQ. Gọi N là giao điểm thứ hai của đường tròn (O;R). Tia PN cắt đường thẳng AQ tại K
Câu hỏi số 1:
Chứng minh tứ giác APOQ là tứ giác nội tiếp và KA2 = KN.KP
Câu hỏi số 2:
Kẻ đường kính QS của đường tròn (O;R). Chứng minh NS là tia phân giác của góc PNM
Câu hỏi số 3:
Gọi G là giao điểm của 2 đường thẳng AO và PK. Tính độ dài đoạn thẳng AG theo bán kính R
Bài 60:
Cho hình vuông ABCD có độ dài cạnh bằng a. Trên cạnh AD và CD lầ lượt lấy các điểm M và N sao cho 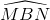 = 450.BM và BN cắt AC theo thứ tự E và F
= 450.BM và BN cắt AC theo thứ tự E và F
Câu hỏi số 1:
Chứng minh các tứ giác ABFM, BCNE, MEFN nội tiếp
Câu hỏi số 2:
Gọi H là giao điểm của MF với NE và I là giao điểm của BH với MN. Tính độ dài đoạn BI theo a
Câu hỏi số 3:
TÌm vị trí của M và N sao cho diện tích tam giác MDN lớn nhất
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









