Bất Đẳng thức, Giá trị lớn nhất và nhỏ nhất
Chuyên đề này giới thiệu một số bài toán về Bất Đẳng thức, các bài toán tính Giá trị lớn nhất và nhỏ nhất, ôn tập rèn luyện kỹ năng giải một số
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 41:
Chứng minh rằng a > 0, b > 0, c > 0 thì
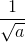 +
+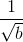 +
+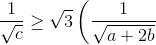 +
+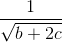 +
+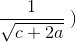
Câu hỏi số 42:
Cho 3 số dương x, y , z có tổng bằng 1. Chứng minh bất đẳng thức:
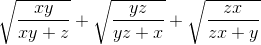 ≤
≤ 
Câu hỏi số 43:
Cho các số a, b, c dương thỏa mãn điều kiện a + b + c = 2. Tìm giá trị lớn nhất của S =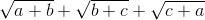
Câu hỏi số 44:
Cho a, b, c là ba số thực dương thỏa mãn abc = 1.
Chứng minh rằng: 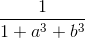 +
+ 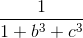 +
+ 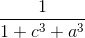 ≤ 1
≤ 1
Câu hỏi số 45:
Cho a, b, c là 3 số thực không âm có tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức : F =(1 + a2) (1 + b2) (1 + c2)
Câu hỏi số 46:
Cho x, y, z là các số thực dương thỏa mãn : 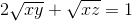
Tìm giá trị nhỏ nhất của biểu thức : .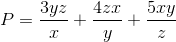
Câu hỏi số 47:
Cho các số thực dương x, y, z thỏa mãn y2 ≥ xz và z2 ≥ xy. Tìm giá trị nhỏ nhất của biểu thức : P = 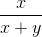 +
+ 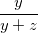 +
+ 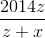 .
.
Câu hỏi số 48:
Cho a, b, c là các số thực dương có tổng bằng 1.
Chứng minh rằng: 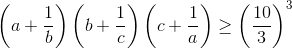
Câu hỏi số 49:
Cho a, b, c ε [1; 2]. Tìm giá trị nhỏ nhất của biểu thức:
P = 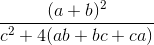
Câu hỏi số 50:
Cho các số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức:
P = 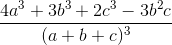
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









