Hệ thức lượng trong tam giác vuông
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 31:
Cho ∆ABC có 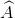 = 750, AB = 10 cm. Số đo các góc
= 750, AB = 10 cm. Số đo các góc 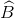 và
và ![]() tỉ lệ với 4 và 3. Tính độ dài các cạnh CA, CB, và SABC.
tỉ lệ với 4 và 3. Tính độ dài các cạnh CA, CB, và SABC.
Câu hỏi số 32:
Tam giác ABC có AB = 3 cm, AC = 6 cm, 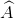 = 1200. Kẻ đường phân giác AD của
= 1200. Kẻ đường phân giác AD của 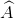 . Tính độ dài của AD.
. Tính độ dài của AD.
Câu hỏi số 33:
Cho ∆ABC có 3 góc nhọn, các cạnh đối diện với các góc 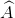 ,
, 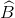 ,
, 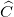 theo thứ tự là a, b, c
theo thứ tự là a, b, c
Chứng minh rằng: 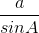 =
= 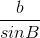 =
= 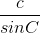
Câu hỏi số 34:
Cho ∆ABC (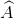 < 900). Trên cạnh AB lấy điểm B', trên cạnh AC lấy điểm C'. Chứng minh:
< 900). Trên cạnh AB lấy điểm B', trên cạnh AC lấy điểm C'. Chứng minh: 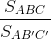 =
= 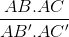 (SABC và SAB’C’ là diện tích ∆ABC và ∆AB'C')
(SABC và SAB’C’ là diện tích ∆ABC và ∆AB'C')
Câu hỏi số 35:
Tứ giác ABCD có hai đường chéo cắt nhau tại O, tạo thành góc nhọn AOD. Chứng minh: SABCD =  AC.BD.sin
AC.BD.sin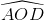
Áp dụng: Cho hình vuông ABCD (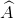 =
= 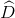 = 900), AB = 12 cm, AD = 9 cm, DC = 18 cm. Hai đường chéo cắt nhau tại O. Tính sin
= 900), AB = 12 cm, AD = 9 cm, DC = 18 cm. Hai đường chéo cắt nhau tại O. Tính sin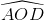
Câu hỏi số 36:
Cho hình bình hành ABCD có 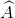 < 900. Chứng minh diện tích của hình đó là S = AB.AD.sinA
< 900. Chứng minh diện tích của hình đó là S = AB.AD.sinA
Áp dụng: Biết SABCD = 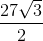 (cm2), AB = 4,5 cm, AD = 6 cm. Tính số đo các góc của hình bình hành ABCD.
(cm2), AB = 4,5 cm, AD = 6 cm. Tính số đo các góc của hình bình hành ABCD.
Câu hỏi số 37:
Cho tam giác ABC có góc A nhọn. Chứng minh diện tích tam giác đó là:
S =  AB.AC.sinA
AB.AC.sinA
Áp dụng:
a. Tính SABC biết AB = 4cm, AC = 7cm và 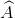 = 600.
= 600.
b. Biết SABC = 5√2 (cm2), AB = 4 cm, AC = 5 cm. Tính số đo của 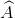
Câu hỏi số 38:
Cho tam giác vuông ABC (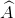 = 900), đường cao AH, CH = 4,9 cm, sinB =
= 900), đường cao AH, CH = 4,9 cm, sinB = 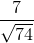
a. Tính các tỉ số lượng giác của 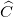
b. Tính diện tích ∆ABC.
Câu hỏi số 39:
Cho tam giác vuông ABC (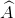 = 900). Biết tgB = √2.
= 900). Biết tgB = √2.
a. Tính các tỉ số lượng giác của 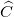
b. Kẻ AH ⊥ BC. Biết AH = 2√3 cm. Tính các cạnh của ∆ABC.
Câu hỏi số 40:
Cho ∆ABC có 3 góc nhọn. Kẻ các đường cao AD; BE; CF. Chứng mih rằng:
AD.BE.CF = AB.AC.BC.sinA.sinB.sinC = AB.AC.BC.cos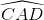 .cos
.cos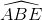 .cos
.cos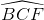
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









